Question 1196998: A cone-shaped paper drinking cup is to hold 40cm^3 of water. Find the height and radius of the cup that will require the least amount of paper. NOTE: Enter the exact answers.
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A cone-shaped paper drinking cup is to hold 40cm^3 of water.
Find the height and radius of the cup that will require
the least amount of paper. NOTE: Enter the exact answers.
~~~~~~~~~~~~~~~~
The "solution" by @ewatrrr is INCORRECT.
It is incorrect, since she uses the formula for the total surface area of the cone,
including its base, while in this problem the area of the base of the cone should NOT be included
and should not be considered, at all.
So, I came to bring a correct solution.
The volume of the cone cup is given 40 cm^3.
The lateral area of a cone is
S = 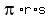 , (1)
where r is the base radius and "s" is the slant height: s = , (1)
where r is the base radius and "s" is the slant height: s = 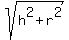 .
So, we need minimize the lateral area
S = .
So, we need minimize the lateral area
S = 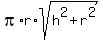 (2)
at given restriction for the volume (2)
at given restriction for the volume
 = 40 cm^3. (3)
From the restriction (3),
h = = 40 cm^3. (3)
From the restriction (3),
h =  .
We substitute it into expression (2), and we get S(r) as a function of the radius r, only
S(r) = .
We substitute it into expression (2), and we get S(r) as a function of the radius r, only
S(r) = 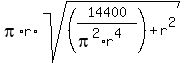 = =  +-------------------------------------------------------+
| To find the minimum of S(r), we should calculate |
| the derivative and equate it to zero. |
+-------------------------------------------------------+
I will not calculate the derivative in full, which is a complicated fraction.
It is enough to calculate its numerator and equate it to zero. It gives this equation
-
+-------------------------------------------------------+
| To find the minimum of S(r), we should calculate |
| the derivative and equate it to zero. |
+-------------------------------------------------------+
I will not calculate the derivative in full, which is a complicated fraction.
It is enough to calculate its numerator and equate it to zero. It gives this equation
-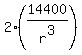 + + 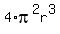 = 0,
or, equivalently
7200 = = 0,
or, equivalently
7200 = 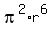 , , 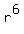 = = 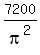 , r = , r = 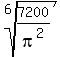 = 3.0 cm. (4)
So, the radius is just found. The height should be
h = = 3.0 cm. (4)
So, the radius is just found. The height should be
h =  = = 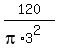 = 4.24 cm. (5)
Expressions (4) and (5) give the required exact formulas and approximate numerical values. = 4.24 cm. (5)
Expressions (4) and (5) give the required exact formulas and approximate numerical values.
Solved.
-------------------
For your safety, ignore the post by @ewatrrr, since her solution is incorrect.
From day to day, this woman repeats the same error: she tries to solve problems that are out of her competency.
|
|
|