Question 1192200: Given a circle with sector AOB, centre O, radius r cm, where the acute angle AOB is θ radians. Given
that the perimeter of the sector is 14 cm and the area of the sector is 10 cm^2, evaluate r and θ
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given a circle with sector AOB, centre O, radius r cm, where the acute angle AOB is θ radians. Given
that the perimeter of the sector is 14 cm and the area of the sector is 10 cm^2, evaluate r and θ
~~~~~~~~~~~~~~~~~~~~
The arc length is  ; the sector area is ; the sector area is 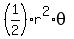 .
Therefore, the equations for the problem are
2r + .
Therefore, the equations for the problem are
2r + 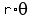 = 14 cm (the perimeter) (1) = 14 cm (the perimeter) (1)
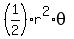 = 10 cm^2 (the area) (2)
To find r, multiply equation (1) by r. You will get = 10 cm^2 (the area) (2)
To find r, multiply equation (1) by r. You will get
 + +  = 14r. (3)
In (3), replace = 14r. (3)
In (3), replace  by 20, based on (2). You will get by 20, based on (2). You will get
 + 20 = 14r,
or + 20 = 14r,
or
 - 14r + 20 = 0, - 14r + 20 = 0,
 - 7r + 10 = 0,
(r-5)*(r-2) = 0,
so the roots of (3) are r= 2 and r= 5.
If r = 2, then from (2) - 7r + 10 = 0,
(r-5)*(r-2) = 0,
so the roots of (3) are r= 2 and r= 5.
If r = 2, then from (2)  = =  = 5 radians.
If r = 5, then from (2) = 5 radians.
If r = 5, then from (2)  = = 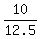 = 0.8 radians.
Thus the problem has two solutions.
One solution is r= 2 cm, = 0.8 radians.
Thus the problem has two solutions.
One solution is r= 2 cm,  = 5 radians.
Other solution is r= 5 cm, = 5 radians.
Other solution is r= 5 cm,  = 0.8 radians. = 0.8 radians.
Solved.
|
|
|