Question 1179135: Prove 4•10^(2n)+9•10^(2n-1)+5 is divisible by 99 for n is in N.
Found 3 solutions by greenestamps, MathLover1, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Use mathematical induction....
(1) show it is true for n=1; then (2) show that if it is true for n=k then it is also true for n=k+1
(1) When n=1, the expression is 4(100)+9(10)+5 = 495 = 5(99).
The expression is divisible by 99 for n=1.
(2) Assume the expression is true for n=k and show that it follows that it is true for n=k+1:
Assume 4*10^(2k)+9*10(2k-1)+5 is divisible by 99. Then
4*10^(2(k+1))+9*10^(2(k+1)-1)+5 =
4*10^(2k+2)+9*10^(2k+1)+5 =
100(4*10^(2k)+9*10(2k-1)+5)-495
In that expression, (4*10^(2k)+9*10(2k-1)+5) is divisible by 99 and 495 is also divisible by 99, so we have shown that if the expression is true for n=k then it follows that it is true for n=k+1.
That completes the proof by mathematical induction.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Prove 4•10^(2n)+9•10^(2n-1)+5 is divisible by 99 for n is in N.
~~~~~~~~~~~~~~
The given number is
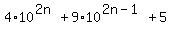 . (1)
+---------------------------------------------------------------+
| Notice that the number . (1)
+---------------------------------------------------------------+
| Notice that the number 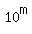 gives the remainder 1, |
| when is divided by 9, for ANY positive integer m. |
+---------------------------------------------------------------+
It implies that the first addend in (1) gives the remainder 4, when is divided by 9.
The second addend in (1) is divisible by 9 without the remainder (OBVIOUSLY).
It makes it OBVIOUS that the number (1) is divisible by 9 without the remainder.
Next, the number (1) has the form 49000 . . .005, where
- the leading digit 4 is located in some O D D position (2n+1), counting from the most right "ones" position;
- the digit 9 is placed in the next (E V E N) position (2n);
- and the last, "ones" digit 5 is located in the most right position number ONE (counting from the right);
- while all the other digits are zeros.
Applying the "divisibility by 11 rule", we see that the number (1) has alternate sum of digits 4 - 9 + 5 = 0.
Since the alternate sum of digits equal 0 (i.e. is divisible by 11),
it means that the number (1) itself is divisible by 11,
according to the "divisibility by 11 rule.
Thus the number (1) is multiple of 9 and 11 --- HENCE, it is multiple of 99. gives the remainder 1, |
| when is divided by 9, for ANY positive integer m. |
+---------------------------------------------------------------+
It implies that the first addend in (1) gives the remainder 4, when is divided by 9.
The second addend in (1) is divisible by 9 without the remainder (OBVIOUSLY).
It makes it OBVIOUS that the number (1) is divisible by 9 without the remainder.
Next, the number (1) has the form 49000 . . .005, where
- the leading digit 4 is located in some O D D position (2n+1), counting from the most right "ones" position;
- the digit 9 is placed in the next (E V E N) position (2n);
- and the last, "ones" digit 5 is located in the most right position number ONE (counting from the right);
- while all the other digits are zeros.
Applying the "divisibility by 11 rule", we see that the number (1) has alternate sum of digits 4 - 9 + 5 = 0.
Since the alternate sum of digits equal 0 (i.e. is divisible by 11),
it means that the number (1) itself is divisible by 11,
according to the "divisibility by 11 rule.
Thus the number (1) is multiple of 9 and 11 --- HENCE, it is multiple of 99.
Solved (mentally), explained and completed.
------------------
On the "divisibility by 11 rule" see the lesson
- Divisibility by 11 rule
in this site.
*******************************************************
An integer number is divisible by 11 if and only if
the alternate sum of its digits is divisible by 11.
*******************************************************
|
|
|