.
To simplify my writing/printing/typing, I will use notations "a" and "b" instead of 
and 
, respectively.
So, the problem is
If "a" and "b" are roots of 2x² - 35x + 2 = 0, find the value of (2a - 35)³(2b - 35)³.
Solution
Since "a" is the root, we have 2a^2 - 35a + 2 = 0, or 2a^2 - 35a = -2, which is the same as
a*(2a-35) = -2, or 2a-35 =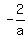 
(1)
Since "b" is the root, we have 2b^2 - 35b + 2 = 0, or 2b^2 - 35b = -2, which is the same as
b*(2b-35) = -2, or 2b-35 =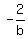 
(2)
Now, since "a" and "b" are the roots of the equation 2x^2 - 35x + 2 = 0,
we have, due to the Vieta's theorem, ab =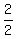 
= 1.
Therefore, (2a-35)*(2b-35) =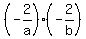 
= 
= 
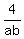= 4.
After that, there is only one step to get the answer, and this step is to cube the last equation
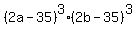= 4^3 = 64.
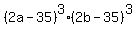ANSWER. Under given conditions, = 64.
Solved.
