SOLUTION: A rectangular area of 1,050 square feet is to be enclosed by a fence, then divided down the middle by another piece of fence. The fence down the middle costs $0.50 per running foot

From the context, the dimensions of the rectangle are not given for advance - they are unknowns and they should be found

from the minimum cost condition.


Let x be one dimension and y be the other dimension of the rectangle.


Then the cost of the outside perimeter fence is 1.50*(2x+2y) dollars = 3*(x+y) dollars,

while the cost of the fence down middle is 0.50*x dollars.


    Note, that I don't know now, which dimension will be the length and which be the width.

    When the problem will be solved, the solution will tell me it . . . 


So, I need minimize the function  

        f(x,y) = 3*(x+y) + 0.5x     (1)

under the condition

        x*y = 1050.                 (2)



From (2), express  y = 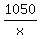  and substitute it into (1). You will get

        g(x) =  =  +  + .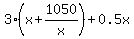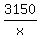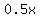


Differentiate it over x

        g'(x) =  -  +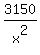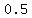 

and equate the derivative to zero.  You will get


        3.5 = 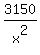,    or

        3.5x^2 = 3150

           x^2 = 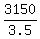 = 900,

           x  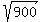 =  = 30.


Thus the dimensions of the rectangle are 30 ft  and 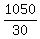  = 35 ft.

The fence down middle has the length of 30 ft;  hence, it is parallel to the shorter side of the rectangle.