Question 1146973: if x = (a + (a²+b³)^1/2)^1/3 + (a - (a²+b³)^1/2)^1/3) then x³ + 3bx ise
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
Answer by ikleyn(52876)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Looking into the solution by Edwin, not every school student knows about the formula Cardano.
So, I think, more simple and more accessible solution is expected and is required.
See such a solution below. It uses nothing that goes outside of the standard school Math curriculum.
Nothing --- except combining standard knowledge in the right order :)
I will introduce new variables u =  and v = and v =  .
Then .
Then
 = = 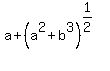 , ,
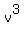 = = 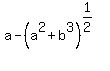 ,
x = u + v, ,
x = u + v,
 = =  . . = =  = = 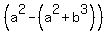 = = 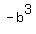 ;
therefore, ;
therefore, 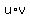 = =  = -b.
Thus we have x = u + v, = -b.
Thus we have x = u + v,  + + 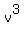 = 2a, and u*v = -b. (1)
Next, = 2a, and u*v = -b. (1)
Next,  = = 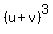 = =  + +  + + 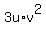 + + 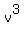 = =  + +  .
Substitute here from (1), and you will get .
Substitute here from (1), and you will get
 = 2a + 3*(-b)*x = 2a - 3bx.
Therefore, = 2a + 3*(-b)*x = 2a - 3bx.
Therefore,
 + 3bx = 2a. ANSWER + 3bx = 2a. ANSWER
Completed and solved, and an ELEMENTARY solution is obtained.
|
|
|