Question 1140061: If 2^x = 4^y = 8^z and 1/(2x) + 1/(4y) + 1/(8z) = 22/7. Show that x = 7/16, y = 7/32 and z = 7/48.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! ONE WAY:
We know  , , 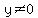 and and 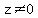 because otherwise they would make the denominators zero, and the expression because otherwise they would make the denominators zero, and the expression  would not exist as a real number. would not exist as a real number.
As  and and  , ,
if  , ,
 , ,
and  , ,  , and , and  . .
Also  , which means , which means  , and , and  . .
You could also talk about taking logarithms base 2.\ to get to the same conclusions.
Then, substituting into  , we get , we get




Multiplying both sides of the equation times the non-zero number 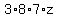 , ,
we get the equivalent equation





Then, as  , ,  , ,
and as  , , 
|
|
|