Question 1026655: When the original price of an item is increased by a certain rate, the increased price is P3100. When the original price is decreased by the same rate, the decreased priced is P 1900. What is the original price of the item?
Found 3 solutions by josgarithmetic, ikleyn, robertb:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52810)  (Show Source):
You can put this solution on YOUR website! .
When the original price of an item is increased by a certain rate, the increased price is P3100.
When the original price is decreased by the same rate, the decreased priced is P 1900. What is the original price of the item?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The equations are
p*r = 3100, (1) ("When the original price of an item is increased by a certain rate, the increased price is P3100.")
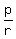 = 1900. (2) ("When the original price is decreased by the same rate, the decreased priced is P 1900.")
Here "p" is the original price, and "r" is the rate.
To find p, multiply equations (1) and (2). You will get
 = 3100*1900.
Now take the square root of both sides. You will get the answer.
The other tutor solved it by another way.
Simply because we differently interpret the term "rate".
Answer by robertb(5830)  (Show Source):
|
|
|
