Question 101529: The length of a rectangle is
1 cm longer than the width.
If the DIAGONAL of the rectangle is 4 cm,
what are the dimensions
(of the length and width)
of the rectangle??
I can get my answer of
2.284 cm and 3.284 cm
but...
I need to show step by step how I got my answer,
this is where I keep writing it out wrong.
Please help...
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! This can be solved using the Pythagorean theorem which states that in a right triangle
having legs A and B and hypotenuse C, then:
.

.
In this problem, the two legs of the right triangle are the width and the length of the
rectangle, and the hypotenuse is the diagonal.
.
The problem tells you that the diagonal is 4 cm. Substitute that value in for C, the hypotenuse,
and the equation becomes:
.

.
The problem also tells you that if W represents the width of the rectangle, then W+1 is
the length because the length is 1 cm more than the width. So substitute W and W+1 into
the Pythagorean theorem and you then have:
.

.
On the left side if you square out 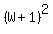 you get you get 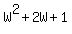 . Substitute . Substitute
this and the equation then becomes:
.

.
On the left side, combine the two  terms and the equation is then: terms and the equation is then:
.

.
Square the right side:
.

.
Get rid of the 16 on the right side by subtracting 16 from both sides to get:
.

.
Notice that this is in the standard quadratic form of:
.

.
and, by comparing our equation and the standard form you can see that a = 2, b = 2, c = -15,
and W = x.
.
You can use the quadratic formula to solve this equation. The quadratic formula says that
for equations of the form:  the answers will be given by: the answers will be given by:
.

.
Now all we have to do is to solve our equation is to replace x with W and substitute
the values we got for a, b, and c into the answer form. When you do that you get:
.

.
First, let's simplify the terms under the radical.  and and  . .
Substitute these results and you get:
.

.
The two terms under the radical combine to 124 and the denominator of (2*2 = 4}}}. Substituting
these results into the equation gives:
.

.
Calculator time. The square root of 124 is 11.13552873
.

.
The answer for W must be positive because it makes no sense to have a negative width. So
we can drop the negative sign in front of the 11.13552873 to get:
.

.
Combine the two numbers in the numerator:
.

.
Calculator time. Divide out the fraction on the right side to get:
.

.
which rounds off to the answer you got for the width of 2.284 cm
.
Then all you have to do to find the length is add 1 cm and you get that the length is 3.284 cm.
.
Hope this helps you get it down on paper.
.
|
|
|