Question 1205510: A box contains 10 chocolates, of which 4 are dark chocolates and 6 are milk chocolates. If two chocolates are randomly selected without replacement, what is the probability of getting one dark chocolate and one milk chocolate in any order?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A box contains 10 chocolates, of which 4 are dark chocolates and 6 are milk chocolates.
If two chocolates are randomly selected without replacement, what is the probability
of getting one dark chocolate and one milk chocolate in any order?
~~~~~~~~~~~~~~~~~~~~~~~~~
The number of all possible different pairs without looking the order
is the number of combinations of 10 items taken 2 at a time
total =  = =  = 5*9 = 45.
The number of pairs (dark,milk), in this order, is 4*6 = 24;
the number of pairs (milk,dark), in this order, is 6*4 = 24;
but since the order does not matter, we DO NOT ADD 24 + 24 - we simply take/keep the value of 24
for all possible different pairs (dark,milk) or (milk,dark) of favorable pairs
favorable = 6*4 = 24.
The probability under the problem's question is
P = = 5*9 = 45.
The number of pairs (dark,milk), in this order, is 4*6 = 24;
the number of pairs (milk,dark), in this order, is 6*4 = 24;
but since the order does not matter, we DO NOT ADD 24 + 24 - we simply take/keep the value of 24
for all possible different pairs (dark,milk) or (milk,dark) of favorable pairs
favorable = 6*4 = 24.
The probability under the problem's question is
P =  = = 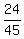 = =  . ANSWER . ANSWER
Solved.
|
|
|