Question 1197033: The elevator at the Matthews Building of the University of New South Wales starts with 10 passengers at the ground and makes stops at each of the 14 floors above. Assuming that it is equally likely that a passenger gets off at any of these 14 floors, what is the probability that at least two of these passengers will get off at the same floor?
Answer by ikleyn(53325)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The elevator at the Matthews Building of the University of New South Wales
starts with 10 passengers at the ground and makes stops at each of the 14 floors above.
Assuming that it is equally likely that a passenger gets off at any of these 14 floors,
what is the probability that at least two of these passengers will get off at the same floor?
~~~~~~~~~~~~~
This problem is the same as the problem on having birthdays in the same day
for a company of k people, and it is solved in the same way - see below.
For 10 passengers, make all possible lists/schedules, at which of 14 floors above
they can get off.
1st passenger can get off at any of 14 floors above, giving 14 options.
2nd passenger can get off at any of 14 floors above, giving 14 options.
3rd passenger can get off at any of 14 floors above, giving 14 options.
. . . . . . . and so on . . . . . . .
10th passenger can get off at any of 14 floors above, giving 14 options.
So, in all, there are  different possible schedules.
Next, let's calculate, how many of these schedules have different floors for different people.
1st passenger can get off at any of 14 floors above, giving 14 options.
2nd passenger can get off at any of remaining 13 floors, giving 13 options.
3rd passenger can get off at any of remaining 12 floors, giving 12 options.
. . . . . . . and so on . . . . . . .
10th passenger can get off at any of remaining 14-9 = 5 floors, giving 5 options.
So, the number of schedules that have have different floors for different people is 14*13*12*. . . *5.
Thus, the probability that no two passengers get out on some floor is different possible schedules.
Next, let's calculate, how many of these schedules have different floors for different people.
1st passenger can get off at any of 14 floors above, giving 14 options.
2nd passenger can get off at any of remaining 13 floors, giving 13 options.
3rd passenger can get off at any of remaining 12 floors, giving 12 options.
. . . . . . . and so on . . . . . . .
10th passenger can get off at any of remaining 14-9 = 5 floors, giving 5 options.
So, the number of schedules that have have different floors for different people is 14*13*12*. . . *5.
Thus, the probability that no two passengers get out on some floor is
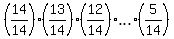 = 0.01256 (rounded).
From here, the probability that at least two of these passengers will get off
at the same floor is the COMPLEMENT of this value to 1
P = 1 - = 0.01256 (rounded).
From here, the probability that at least two of these passengers will get off
at the same floor is the COMPLEMENT of this value to 1
P = 1 - 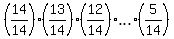 = 1 - 0.01256 = 0.98744 (rounded).
ANSWER. The probability that at least two of these passengers will get off at the same floor is
P = 1 - = 1 - 0.01256 = 0.98744 (rounded).
ANSWER. The probability that at least two of these passengers will get off at the same floor is
P = 1 - 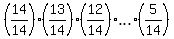 = 1 - 0.01256 = 0.98744 (rounded) = 1 - 0.01256 = 0.98744 (rounded)
Solved.
|
|
|