Question 1183581: From actual road tests with the tires, Hankook Tires estimated that the mean tire mileage is 36,500 miles and that the standard deviation is 5000 miles. Data is normally distributed.
(i) What percentage of the tires can be expected to last more than 40,000 miles?
(ii) Assume that Hankook Tires is considering a guarantee that will provide a discount on replacement tires if the original tires do not provide the guaranteed mileage. What should the guarantee mileage be if the company wants no more than 10% of the tires to be eligible for the discount guarantee?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the mean is 36500.
the standard deviation is 5000.
z = (x - m) / s
z is the z-score
x is the raw score
m is the raw mean
s is the standard deviation.
z = (40000 - 36500) / 5000 = .7
the area to the left of a z-score of .7 is equal to .7580364218.
round to 4 decimal places to get .7580.
.7580 * 100 = 75.8% of the tires will not last more than 40000 miles.
that means that 100% - 75.8% = 24.2% will last more than 40000 miles.
for 10% of the tires not to last more than the guaranteed mileage, the guaranteed mileage needs to have a z-score of
if they guarantee the tires to last more than 42907.75 miles, then they will only have to provide a discount for 10% of the tires.
the required z-score will be equal to -1.28155 rounded to 5 decimal places.
use the z-score formula to find the raw score.
z = (x - 36500) / 5000 becomes -1.28155 = (x - 36500) / 5000.
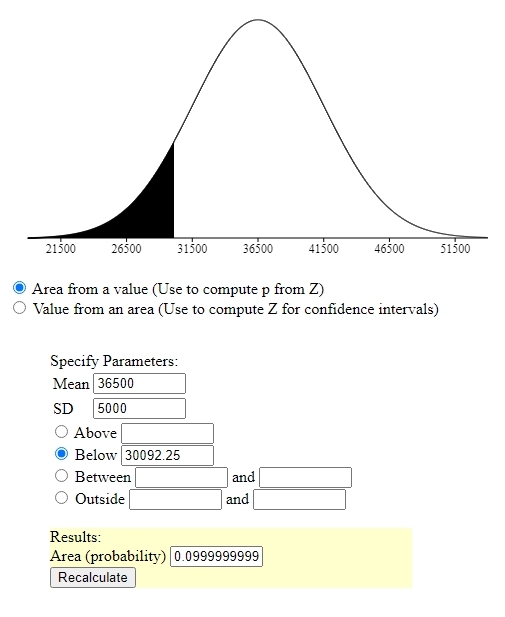
solve for x to get x = -1.28155 * 5000 + 36500 = 30092.25.
if they guarantee the tires to last at least 30092.25 miles, then they will only have to provide a discount for 10% of the tires.
these results can be seen in the following displays.
the first display shows the ratio of tires not lasting more than 40000 miles.
the second display shows the percent tires that will not last more than 42909.4 miles.

Answer by ikleyn(53570)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From actual road tests with the tires, Hankook Tires estimated that the mean tire mileage is 36,500 miles
and that the standard deviation is 5000 miles. Data is normally distributed.
(i) What percentage of the tires can be expected to last more than 40,000 miles?
(ii) Assume that Hankook Tires is considering a guarantee that will provide a discount on replacement tires
if the original tires do not provide the guaranteed mileage. What should the guarantee mileage be
if the company wants no more than 10% of the tires to be eligible for the discount guarantee?
~~~~~~~~~~~~~~~~
I think that the basic assumption made in this problem that the tire mileage is described by the normal distribution
is INCORRECT and CONTRADICTS to COMMON SENSE, as well as to the MATERIAL SCIENCE.
THEREFORE, I think, the problem, as it is worded, printed, posted and presented, is a FAKE.
/////////////
It is the same as to assume that the age of people is distributed normally, which is, OBVIOUSLY, not a case.
|
|
|