Question 1179519: A man gets a raise of 12% in salary at end of first year and further raises of 16% ,19% and 25% at the end of second, third and fourth years respectively; the raise in each year being calculated on his salary at the beginning of the year. What is the average annual percentage increase?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
@greenestamps correctly noticed that this problem formulation admits SEVERAL different interpretations.
I came with my own interpretation and with my own solution.
After the 1st year, the salary is 1.12 of the original salary.
After the 2nd year, the salary is 1.16*1.12 of the original salary.
After the 3rd year, the salary is 1.19*1.16*1.12 of the original salary.
After the 4th year, the salary is 1.25*1.19*1.16*1.12 of the original salary.
So, after 4 years, the salary is 1.25*1.19*1.16*1.12 = 1.93256 of the original salary.
They want you to find an EQUIVALENT annual growth coefficient that provides this calculated increase of salary in four years.
For it, you should solve this equation
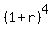 = 1.93256.
It is easy to do:
1 + r =  = 1.179 (rounded).
It gives then average annual percentage increase r = 1.179 - 1 = 0.179, or 17.9%. ANSWER
Solved, with my interpretation N 3.
|
|
|
