Question 1099250: Can someone help me? Thank you.
A production line produces bags of sugar that follow a normal distribution with a mean weight of 1.01kg and a standard deviation of 0.02kg.
If P(X≥b)=0.9330, then what is the value of b?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! mean is 1.01 kg.
standard deviation is .02 kg.
you want to find b in the formula p(x >= b) = .9330
you can use a z-score calculator find p(x >= b) = .9330.
that will tell you the z-score associated with an area under the normal distribution curve that is to the right of that z-score.
the area to the right of any z-score is equal to 1 minus the area to the left of that z-score.
therefore you are looking for an area to the left of the z-score equal to 1 - .9330 = .0670.
without getting into the details of how i found that just yet, the z-score would be equal to -1.499
that would be the z-score that had an area to the right of it of .9330, or equivalently, an area to the left of it of .0670.
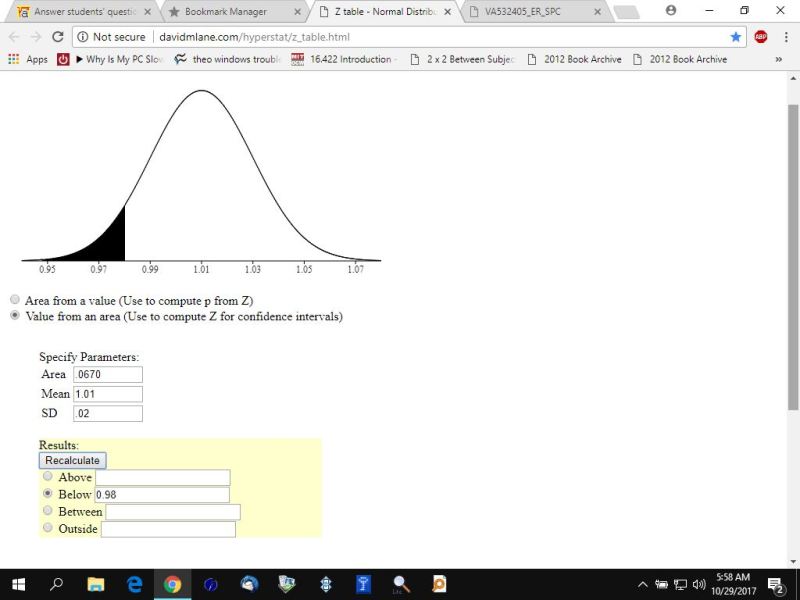
the following pictures from an online z-score calculator show that to be true.
the first picture looks for an area to the right of .9330.
the second picture looks for an area to the left of .0670


i used my TI-84 PLUS scientific calculator to find the z-score and i got a z-score of -1.498513067 which can be rounded to -1.499.
the online z-score distribution calculator can be found at http://davidmlane.com/hyperstat/z_table.html
the TI-84 PLUS can be found on EBAY at a reasonable cost (used).
i paid around $40 for mine.
you can also use z-score tables to find the result manually.
one such table can be found at http://www.stat.ufl.edu/~athienit/Tables/Ztable.pdf
using this table, i looks for an area under the normal distribution curve to the left of the indicated z-score of .0670.
the translation was necessary since the table only shows the area to the left of the indicated z-score.
i found that an area to the left of .0681 gave me a z-score of -1.49 and an area to the left of .0668 gave me a z-score of -1.5.
a manual interpolation to find the z-score for an area to the left of that z-score of .0670 yielded -1.498 which is very close to the mechanically generated z-score of -1.499.
the difference has to do with rounding and interpolation techniques.
the mechanically generated results are more accurate.
once the z-score is found, then you need to find the raw score correlated to that.
the formula for z-score is z = (x-m)/s
x is the raw score.
z is the z-score.
m is the mean.
s is the stnadard deviation.
you are given the mean is 1.01 kg.
you are given the standard deviation is .02 kg.
you have found that the z-score is -1.499
the formula becomes -1.499 = (x-1.01) / .02
solve for x to get x = .02 * -1.499 + 1.01.
this gets you x = .98002 kg which can be rounded to .98 kg
the online normal distribution calculator shows this to be true.
using the calculator this way, you simply replace 0 with the actual mean and 1 with the actual standard deviation.
here's what the online normal distribution calculator shows when you do that.
any questions about how to do any of this, just send me an email with your questions and i'll explain as best i can.
your questions asked you the following:
A production line produces bags of sugar that follow a normal distribution with a mean weight of 1.01kg and a standard deviation of 0.02kg.
If P(X≥b)=0.9330, then what is the value of b?
if b is the z-score, then the answer would be b = -1.499.
if b is the raw score, then the answer would be b = .98 kg.
i believe they're looking for the raw score, so b = .98 is probably that.
|
|
|