Tutors Answer Your Questions about Normal-probability (FREE)
Question 1170505: A machine fills pop bottles with a standard deviation of 25 mL no matter what the setting is for the mean. At how many mililiters should the mean be set, so that 90% of the bottles will contain at least 500 mL?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let X be the amount of liquid filled in the pop bottles. We are given:
* Standard deviation (σ) = 25 mL
* We want 90% of the bottles to contain at least 500 mL, which means P(X ≥ 500) = 0.90.
We want to find the mean (μ) such that this condition is satisfied.
**1. Convert to Standard Normal Distribution**
We can standardize the random variable X using the formula:
Z = (X - μ) / σ
where Z follows a standard normal distribution (mean 0, standard deviation 1).
We want P(X ≥ 500) = 0.90. Let's rewrite this in terms of Z:
P((X - μ) / σ ≥ (500 - μ) / 25) = 0.90
P(Z ≥ (500 - μ) / 25) = 0.90
**2. Find the Z-score**
We need to find the z-score such that the area to the right of it is 0.90. This means the area to the left of it is 1 - 0.90 = 0.10.
Using a standard normal distribution table or a calculator, we find the z-score corresponding to a cumulative probability of 0.10. This z-score is approximately -1.28.
So, (500 - μ) / 25 = -1.28.
**3. Solve for μ**
Now, we solve for μ:
500 - μ = -1.28 * 25
500 - μ = -32
μ = 500 + 32
μ = 532
**4. Answer**
The mean should be set to 532 mL.
**Therefore, the mean should be set to 532 mL so that 90% of the bottles contain at least 500 mL.**
Question 1199038: Pasien Dirawat di IGD Rumah Sakit Di sebuah rumah sakit, sampel 8 minggu dipilih, dan ditemukan bahwa rata-rata 438 pasien dirawat di IGD setiap minggu. Standar deviasinya adalah 16. Temukan interval kepercayaan 99% dari rata-rata sebenarnya Asumsikan variabel terdistribusi normal.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! ## Menentukan Interval Kepercayaan 99% untuk Rata-rata Pasien di IGD
### Memahami Masalah
Kita memiliki data sampel dari jumlah pasien yang dirawat di IGD selama 8 minggu. Kita ingin mengetahui rentang nilai yang paling mungkin memuat rata-rata populasi (rata-rata jumlah pasien yang dirawat setiap minggu di IGD secara keseluruhan).
### Data yang Diketahui:
* **Ukuran sampel (n):** 8 minggu
* **Rata-rata sampel (x̄):** 438 pasien/minggu
* **Standar deviasi sampel (s):** 16 pasien/minggu
* **Tingkat kepercayaan:** 99%
### Langkah-langkah:
1. **Tentukan tingkat signifikansi (α):**
* Tingkat signifikansi (α) = 1 - Tingkat kepercayaan = 1 - 0.99 = 0.01
* Karena kita mencari interval dua sisi, maka α/2 = 0.01/2 = 0.005
2. **Temukan nilai z-kritis:**
* Menggunakan tabel distribusi normal standar, kita mencari nilai z yang memiliki luas di ekor kanan sebesar 0.005. Nilai z ini adalah sekitar 2.576.
3. **Hitung margin of error (E):**
* E = z * (s / √n)
* E = 2.576 * (16 / √8) ≈ 14.55
4. **Hitung batas atas dan batas bawah interval:**
* Batas bawah = x̄ - E = 438 - 14.55 ≈ 423.45
* Batas atas = x̄ + E = 438 + 14.55 ≈ 452.55
### Kesimpulan
Dengan tingkat kepercayaan 99%, kita dapat mengatakan bahwa rata-rata sebenarnya jumlah pasien yang dirawat di IGD setiap minggu berada di antara **423.45** dan **452.55** pasien.
**Interpretasi:**
Ini berarti bahwa jika kita mengambil banyak sampel dengan ukuran yang sama dan menghitung interval kepercayaan untuk masing-masing sampel, maka sekitar 99% dari interval-interval tersebut akan mengandung rata-rata populasi yang sebenarnya.
**Catatan:**
* **Asumsi Normalitas:** Asumsi bahwa variabel terdistribusi normal penting untuk menggunakan distribusi z. Jika asumsi ini tidak terpenuhi, kita mungkin perlu menggunakan t-distribusi.
* **Populasi Tak Hingga:** Asumsi ini sering dibuat dalam statistik inferensial. Jika populasi terbatas, koreksi finite-population mungkin diperlukan.
* **Sampel Acak:** Sampel yang diambil haruslah acak untuk memastikan representativitas.
**Dalam konteks rumah sakit:**
Interval kepercayaan ini dapat digunakan oleh pihak rumah sakit untuk:
* **Perencanaan:** Memprediksi jumlah pasien yang mungkin datang setiap minggu dan merencanakan sumber daya yang diperlukan (tenaga medis, obat-obatan, dll.).
* **Evaluasi kinerja:** Membandingkan rata-rata pasien yang dirawat dengan target yang telah ditetapkan.
* **Pengambilan keputusan:** Membantu dalam pengambilan keputusan strategis, seperti perluasan fasilitas atau penjadwalan staf.
**Disclaimer:**
Ini adalah perhitungan sederhana. Dalam praktik sebenarnya, analisis yang lebih mendalam mungkin diperlukan, termasuk mempertimbangkan faktor-faktor lain seperti tren musiman, kejadian khusus (seperti wabah penyakit), dan perubahan dalam kebijakan rumah sakit.
Question 1200376: In a suburban community, 30% of the households use Brand A toothpaste, 27% use Brand B, 25% use Brand C, and 18% use Brand D. In the foul groups of households, the proportions of residents who learned about the brand they use through television advertising are as follows Brand A, 0.10; Brand B, 0.05; Brand C, 0.20; and Brand D, 0.15. In a household selected at random from the community, it is found that residents learned about the toothpaste through television advertising. What is the probability that the brand of toothpaste used in the household is (a) A, (b) B, (c) C, (d)D?
Answer by GingerAle(43)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's calculate the probabilities.
**1. Define Probabilities**
* **Prior Probabilities (Brand Usage):**
* P(A) = 0.30 (Brand A)
* P(B) = 0.27 (Brand B)
* P(C) = 0.25 (Brand C)
* P(D) = 0.18 (Brand D)
* **Likelihoods (Learning through TV):**
* P(TV | A) = 0.10 (Probability of learning about Brand A through TV)
* P(TV | B) = 0.05 (Probability of learning about Brand B through TV)
* P(TV | C) = 0.20 (Probability of learning about Brand C through TV)
* P(TV | D) = 0.15 (Probability of learning about Brand D through TV)
**2. Calculate Joint Probabilities**
* Joint Probability = Prior Probability * Likelihood
* P(A and TV) = P(A) * P(TV | A) = 0.30 * 0.10 = 0.03
* P(B and TV) = P(B) * P(TV | B) = 0.27 * 0.05 = 0.0135
* P(C and TV) = P(C) * P(TV | C) = 0.25 * 0.20 = 0.05
* P(D and TV) = P(D) * P(TV | D) = 0.18 * 0.15 = 0.027
**3. Calculate Total Probability of Learning through TV**
* P(TV) = P(A and TV) + P(B and TV) + P(C and TV) + P(D and TV)
* P(TV) = 0.03 + 0.0135 + 0.05 + 0.027 = 0.1205
**4. Calculate Posterior Probabilities (Using Bayes' Theorem)**
* P(A | TV) = P(A and TV) / P(TV) = 0.03 / 0.1205 ≈ 0.2490
* P(B | TV) = P(B and TV) / P(TV) = 0.0135 / 0.1205 ≈ 0.1120
* P(C | TV) = P(C and TV) / P(TV) = 0.05 / 0.1205 ≈ 0.4149
* P(D | TV) = P(D and TV) / P(TV) = 0.027 / 0.1205 ≈ 0.2241
**Therefore:**
* (a) Probability the brand is A given TV advertising: **0.2490**
* (b) Probability the brand is B given TV advertising: **0.1120**
* (c) Probability the brand is C given TV advertising: **0.4149**
* (d) Probability the brand is D given TV advertising: **0.2241**
**In summary:**
* If a randomly selected household learned about their toothpaste through TV advertising, it is most likely that they use **Brand C** (with a probability of approximately 0.4149).
Question 1206682: You have a deck with 52 cards. what is the probability of you pulling a 7 of spades?
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1205865: Three person are contesting elections from Same consistuency. Mr. X and Mr. Y have same chance of "but Mr. Z has twice the chance winning, but Mr. Z either Mr. X or Mr.Y. What is the probability that;
(i) Mr. Z wins.
(ii) Mr. X does not win.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three person are contesting elections from Same consistuency.
Mr. X and Mr. Y have same chance of "but Mr. Z has twice the chance winning, but Mr. Z either Mr. X or Mr.Y.
What is the probability that;
(i) Mr. Z wins.
(ii) Mr. X does not win.
~~~~~~~~~~~~~~~~~~~~~
How about to write your post in a right way ?
I mean - write right words in a right order, as normal people do it . . .
And do not use unnecessary or wrong words.
Try again.
Question 1205510: A box contains 10 chocolates, of which 4 are dark chocolates and 6 are milk chocolates. If two chocolates are randomly selected without replacement, what is the probability of getting one dark chocolate and one milk chocolate in any order?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A box contains 10 chocolates, of which 4 are dark chocolates and 6 are milk chocolates.
If two chocolates are randomly selected without replacement, what is the probability
of getting one dark chocolate and one milk chocolate in any order?
~~~~~~~~~~~~~~~~~~~~~~~~~
The number of all possible different pairs without looking the order
is the number of combinations of 10 items taken 2 at a time
total =  = =  = 5*9 = 45.
The number of pairs (dark,milk), in this order, is 4*6 = 24;
the number of pairs (milk,dark), in this order, is 6*4 = 24;
but since the order does not matter, we DO NOT ADD 24 + 24 - we simply take/keep the value of 24
for all possible different pairs (dark,milk) or (milk,dark) of favorable pairs
favorable = 6*4 = 24.
The probability under the problem's question is
P = = 5*9 = 45.
The number of pairs (dark,milk), in this order, is 4*6 = 24;
the number of pairs (milk,dark), in this order, is 6*4 = 24;
but since the order does not matter, we DO NOT ADD 24 + 24 - we simply take/keep the value of 24
for all possible different pairs (dark,milk) or (milk,dark) of favorable pairs
favorable = 6*4 = 24.
The probability under the problem's question is
P =  = = 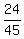 = =  . ANSWER . ANSWER
Solved.
Question 1204966: Business Weekly conducted a survey of graduates from 30 top MBA programs. On the basis of the survey, assume the mean annual salary for graduates 10 years after graduation is 169000 dollars. Assume the standard deviation is 36000 dollars. Suppose you take a simple random sample of 91 graduates. Assume the population is normally distributed.
Note: You should carefully round any intermediate values you calculate to 4 decimal places to match wamap's approach and calculations.
Find the probability that a single randomly selected salary exceeds 166000 dollars.
P(X > 166000) = 0.2023
Enter your answer as a number accurate to 4 decimal places.
Find the probability that a sample of size 91 is randomly selected with a mean that exceeds 166000 dollars.
P(x > 166000) =
Enter your answer as a number accurate to 4 decimal places.
I did the first part but can't find P(xbar > 166000) with sample of 91
part but can not figure out the bottom because when I do it I get a number that does not / can not exist for this problem. please help
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Part 1
mu = 169000 = mean
sigma = 36000 = population standard deviation.
x = 166000
z = (x - mu)/sigma
z = (166000 - 169000)/36000
z = -0.08333333333333 approximately
z = -0.08
Then use Z table to find that P(z < -0.08) = 0.46812 approximately.
Such tables should be found at the back of your stats textbook.
For exams, the teacher will likely hand out the table.
Then,
P(Z > -0.08) = 1-P(Z < -0.08)
P(Z > -0.08) = 1-0.46812
P(Z > -0.08) = 0.53188
This leads back to P(x > 166000) = 0.53188 approximately
Rounding to four decimal places gets us 0.5319
I'm not familiar with wamap, so I don't have access to that particular stats calculator.
However, there are many other available calculators out there as alternatives.
For example, using the TI83 or TI84 gives
normalCDF(-0.08, 99, 0, 1) = 0.531 881 440 4
I put a space between each group of 3 decimal digits to make the number a bit more readable.
That value rounds to 0.5319 when rounding to four decimal places.
Or another TI83 calculation we could do is
normalCDF(-0.0833, 99, 0, 1) = 0.533 205 493 9
That value rounds to 0.5332 when rounding to four decimal places.
Or another TI83 calculation we could do is
normalCDF(-0.083333, 99, 0, 1) = 0.533 206 686 5
That value rounds to 0.5332 when rounding to four decimal places.
It appears that the results steadily approach the value 0.5332 as the z score gets closer to -0.0833333 where the '3's go on forever.
I'm not sure how you came up with 0.2023
Please let me know your scratch work and thought process. Thank you.
Here are some alternative calculators (for future students reading this question who do not have a TI83/TI84 and also don't have access to wamap)- A very user friendly calculator by professor David M Lane. The calculator also displays the shaded diagram which is a nice bonus.
- Use WolframAlpha. Type in P(Z > -0.0833) for instance. Make sure the "referring to statistics" option is selected.
- Use GeoGebra. It can be accessed through either the normal input bar, the CAS mode, or the probability distribution mode. The reference page can be found here
- Use the normDist function on a spreadsheet. See this reference page for more info.
There are many other alternatives that I haven't listed. You can do an internet search to find your favorite one.
Of all of the choices, the 1st option (the David M Lane one) is probably the best for new students.
The only drawback is there doesn't appear to be a way to change the precision.
-------------------------------------------------------------------------
Part 2
mu = 169000 = mean
sigma = 36000 = population standard deviation.
xbar = 166000 = sample mean
n = 91 = sample size
xbar means we have x with a horizontal line over top
When working in the xbar distribution, aka sample mean distribution, we have this z score conversion formula:
z = (xbar - mu)/( sigma/sqrt(n) )
So,
z = (xbar - mu)/( sigma/sqrt(n) )
z = (166000 - 169000)/( 36000/sqrt(91) )
z = -0.79494933451412
z = -0.79
The result is approximate.
Use a table to find that
P(Z < -0.79) = 0.21476
which leads to
P(Z > -0.79) = 1-P(Z < -0.79)
P(Z > -0.79) = 1-0.21476
P(Z > -0.79) = 0.78524
P(Z > -0.79) = 0.7852
and ultimately leads back to
P(xbar > 166000) = 0.7852
If using a TI83, then
normalCDF(-0.7949, 99, 0, 1) = 0.786 664 228 9
and
normalCDF(-0.7949493, 99, 0, 1) = 0.786 678 568 6
Play around with the precision and you'll see the more accurate the input, the results tend to approach 0.7867
It's not too far from the table result 0.7852
Similar calculator results should happen with other calculators.
Question 1204513: The diameter of a brand of tennis balls is approximately normally distributed, with a mean of 2.54 inches and a standard deviation of 0.05 inch. A random sample of 10 tennis balls is selected. What is the probability that the sample mean is less than 2.53 inches?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! population mean is 2.54
population standard deviation is .05
sample size is 10.
standard error is standard deviation / sqrt(sample size) = .0158114.
z = (x - m) / s
z is the z-score
x is the sample mean for test
m is the population mean
s is the standard error.
formula becomes z = (2.53 - 2.54) / .0158114 = - .632455.
area to the left of that z-score under the normal distribution curve is equal to .2635.
this means probability of the mean of a sample of 10 tennis balls having a diameter less than 2.53 is equal to 26.35%.
here's what it looks like on a normal distribution calculator.

Question 1203498: A company estimates that 1% of their products will fail after the original warranty period but within 2 years of the purchase, with a replacement cost of $350.
If they want to offer a 2 year extended warranty, what price should they charge so that they'll break even (in other words, so the expected profit will be 0)
$
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A company estimates that 1% of their products will fail after the original warranty period
but within 2 years of the purchase, with a replacement cost of $350.
If they want to offer a 2 year extended warranty, what price should they charge
so that they'll break even (in other words, so the expected profit will be 0)
~~~~~~~~~~~~~~~~~~~~
The company's cost to replace 1% of their production (which potentially will fail
after the original warranty period but within 2 years of the purchase) is
0.01*350*X dollars, where X is the rate of produced and sold units per year.
Let z be the extended insurance price in dollars per unit.
In order for the profit be zero, this equation should kept
0.01*350*X = z*X,
which gives, after canceling factor X in both sides, z = 0.01*350 = 3.5 dollars per item.
ANSWER. Under given conditions, the extended insurance price is $3.50 per item.
Solved.
Question 1202499: The Great Pyramid of King Khufu was built of limestone in
Egypt over a 20-year time period from 2580 bc to 2560 bc.
Its base is a square with side length 230 m and its height
when built was 147 m. (It was the tallest man-made structure
in the world for more than 3800 years.) The density of
the limestone is about 2400 kg/m3
(a) Estimate the total work done in building the pyramid.
(b) If each laborer worked 10 hours a day for 20 years, for
340 days a year, and did 250 J/h of work in lifting the
limestone blocks into place, about how many laborers
were needed to construct the pyramid?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The Great Pyramid of King Khufu was built of limestone in Egypt over a 20-year time period
from 2580 bc to 2560 bc.
Its base is a square with side length 230 m and its height when built was 147 m.
(It was the tallest man-made structure in the world for more than 3800 years.)
The density of the limestone is about 2400 kg/m3
(a) Estimate the total work done in building the pyramid.
(b) If each laborer worked 10 hours a day for 20 years, for 340 days a year,
and did 250 J/h of work in lifting the limestone blocks into place,
about how many laborers were needed to construct the pyramid?
~~~~~~~~~~~~~~~~~~~~
(a) To answer question (a), find the volume of the pyramid
V = 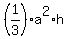 = =  = 2,997,666.667 m^3.
Then multiply the volume by the density to get the mass of the material
M = V*d = 2997666.667*2400 = 7,194,400,001 kilograms.
Then multiply the mass by the gravity acceleration g= 9.81 m/s^2 and by one fourth of the height
to get the work done (the center of the gravity of a pyramid is at 1/4 of the height)
W = = 2,997,666.667 m^3.
Then multiply the volume by the density to get the mass of the material
M = V*d = 2997666.667*2400 = 7,194,400,001 kilograms.
Then multiply the mass by the gravity acceleration g= 9.81 m/s^2 and by one fourth of the height
to get the work done (the center of the gravity of a pyramid is at 1/4 of the height)
W = 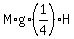 = = 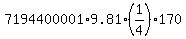 = 2.99953E+12 joules. (1)
It is the ANSWER to question (a).
(b) The work done by one laborer per "year" is
w = 340*10*250 = 850000 joules per laborer per year. (2)
To answer question (b), divide the number W = 2.99953E+12 joules of (1) by 20w,
where w is the number w= 850000 of (2). You will get
the number of laborer = 2.99953E+12 : (20*850000) = 176,443 (rounded).
It is the ANSWER to question (b). = 2.99953E+12 joules. (1)
It is the ANSWER to question (a).
(b) The work done by one laborer per "year" is
w = 340*10*250 = 850000 joules per laborer per year. (2)
To answer question (b), divide the number W = 2.99953E+12 joules of (1) by 20w,
where w is the number w= 850000 of (2). You will get
the number of laborer = 2.99953E+12 : (20*850000) = 176,443 (rounded).
It is the ANSWER to question (b).
Solved.
-----------------------
To read more about this construction. read this Wikipedia article
https://en.wikipedia.org/wiki/Great_Pyramid_of_Giza
Question 1202367: A box contains 4 white shirts and 3 blue shirts. Two shirts are picked at random from the box, one at a time without replacement. What is the probability that the first chip is white and the second chip is blue?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First shirt (not chip) white: There are 7 shirts, of which 4 are white. The probability is 4/7.
Second shirt (not chip) blue: There are 6 shirts left of which 3 are blue. The probability is 3/6 = 1/2.
By the fundamental counting principle, the probability of white first and then blue second is the product of those two probabilities.
ANSWER: (4/7)(1/2) = 2/7
Question 1201898: A class consisting of 8 men and 7 women we're 2 selected randomly to represent the class in a dabate find the probability that the 2 selected are (I) both men (ii) both woman (iii) of the same Sex (iv) of the different Sex.
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1201663: Please solve this equation:
The mean of a normal probability distribution is 300; the standard deviation is 16.
a. About 68% of the observations lie between what two values?
______________
b. About 95% of the observations lie between what two values?
___________________________
c. Practically all of the observations lie between what two values?
_____________________
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:- 284 and 316
- 268 and 332
- 252 and 348
Explanation:
We use the Empirical Rule.
Some textbooks call it the 68-95-99.7 rule but I don't think it's as catchy of a name.
The rule has 3 properties:- roughly 68% of the normal distribution is within 1 standard deviation of the mean.
- roughly 95% of the normal distribution is within 2 standard deviations of the mean.
- roughly 99.7% of the normal distribution is within 3 standard deviations of the mean.

For part (a), the work shown would be something like this
mu - 1*sigma = 300 - 1*16 = 284
mu + 1*sigma = 300 + 1*16 = 316
Roughly 68% of the observations are between 284 and 316.
For part (b), we have
mu - 2*sigma = 300 - 2*16 = 268
mu + 2*sigma = 300 + 2*16 = 332
Roughly 95% of the observations are between 268 and 332.
For part (c), the phrasing "practically all" means "practically 100%" which is close enough to 99.7%
mu - 3*sigma = 300 - 3*16 = 252
mu + 3*sigma = 300 + 3*16 = 348
Roughly 99.7%, aka practically all, of the observations are between 252 and 348.
Question 1201071: 123 year 11 students chose the courses they wanted at the school prom dinner. 75 chose a starter, 106 chose a main course and 81 chose a dessert. 67 chose a main course and dessert, 64 chose a starter and a main course while 49 chose a starter and dessert. Everybody ordered at least one course. Find the probability that a student chosen at random chose all three courses
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1200896: Fair six sided die is rolled four times was the probability that the sequence of rolls is 6234
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 1/1296
Reason:
There are 6^4 = 6*6*6*6 = 1296 ways to roll a die four times.
This is equivalent to having 1296 ways to roll four dice.
Each die has 6 sides. Repeat entries are possible.
Out of those 1296 total outcomes, only one has the sequence 6234. The order matters.
Therefore, 1/1296 is the probability of getting this sequence in the order mentioned.
Question 1197799: A bag of marbles contains 6 blue, 7 red, and 8 orange marbles. What is the probability of picking a red marble and then an orange marble if you do not replace the first marble?
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bag of marbles contains 6 blue, 7 red, and 8 orange marbles. What is the probability of picking a red marble and then an orange marble if you do not replace the first marble?
-----------
It's called "without replacement."
----
The red is 7 of 21.
The orange is 8 of 20.
---
(7/21)*(8/20) = 2/15
Question 1197033: The elevator at the Matthews Building of the University of New South Wales starts with 10 passengers at the ground and makes stops at each of the 14 floors above. Assuming that it is equally likely that a passenger gets off at any of these 14 floors, what is the probability that at least two of these passengers will get off at the same floor?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The elevator at the Matthews Building of the University of New South Wales
starts with 10 passengers at the ground and makes stops at each of the 14 floors above.
Assuming that it is equally likely that a passenger gets off at any of these 14 floors,
what is the probability that at least two of these passengers will get off at the same floor?
~~~~~~~~~~~~~
This problem is the same as the problem on having birthdays in the same day
for a company of k people, and it is solved in the same way - see below.
For 10 passengers, make all possible lists/schedules, at which of 14 floors above
they can get off.
1st passenger can get off at any of 14 floors above, giving 14 options.
2nd passenger can get off at any of 14 floors above, giving 14 options.
3rd passenger can get off at any of 14 floors above, giving 14 options.
. . . . . . . and so on . . . . . . .
10th passenger can get off at any of 14 floors above, giving 14 options.
So, in all, there are  different possible schedules.
Next, let's calculate, how many of these schedules have different floors for different people.
1st passenger can get off at any of 14 floors above, giving 14 options.
2nd passenger can get off at any of remaining 13 floors, giving 13 options.
3rd passenger can get off at any of remaining 12 floors, giving 12 options.
. . . . . . . and so on . . . . . . .
10th passenger can get off at any of remaining 14-9 = 5 floors, giving 5 options.
So, the number of schedules that have have different floors for different people is 14*13*12*. . . *5.
Thus, the probability that no two passengers get out on some floor is different possible schedules.
Next, let's calculate, how many of these schedules have different floors for different people.
1st passenger can get off at any of 14 floors above, giving 14 options.
2nd passenger can get off at any of remaining 13 floors, giving 13 options.
3rd passenger can get off at any of remaining 12 floors, giving 12 options.
. . . . . . . and so on . . . . . . .
10th passenger can get off at any of remaining 14-9 = 5 floors, giving 5 options.
So, the number of schedules that have have different floors for different people is 14*13*12*. . . *5.
Thus, the probability that no two passengers get out on some floor is
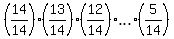 = 0.01256 (rounded).
From here, the probability that at least two of these passengers will get off
at the same floor is the COMPLEMENT of this value to 1
P = 1 - = 0.01256 (rounded).
From here, the probability that at least two of these passengers will get off
at the same floor is the COMPLEMENT of this value to 1
P = 1 - 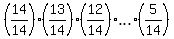 = 1 - 0.01256 = 0.98744 (rounded).
ANSWER. The probability that at least two of these passengers will get off at the same floor is
P = 1 - = 1 - 0.01256 = 0.98744 (rounded).
ANSWER. The probability that at least two of these passengers will get off at the same floor is
P = 1 - 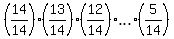 = 1 - 0.01256 = 0.98744 (rounded) = 1 - 0.01256 = 0.98744 (rounded)
Solved.
Question 1195825: Suppose commute times in a large city are normally distributed and that 62.50% of commuters in this city take more than 20 minutes to commute one-way. If the standard deviation of such commutes is 6.5 minutes, what is the mean commute?
Answer by Boreal(15235)   (Show Source): (Show Source):
Question 1194055: Compute the area under the normal curve with the following data: μ=35 and σ=3, when x is more than 30 but less than 40. Round to two decimal places and do not include the "percent sign". *
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Use free of charge online calculator
https://onlinestatbook.com/2/calculators/normal_dist.html
specially intended for this purpose.
Question 1193884: Suppose Z is a standard normal random variable and let Y = aZ +b, where a > 0 and b are constants.
(a) Show that MY (t) = exp {bt +
a
2
t
2
2
}.
(b) Calculate the probability, P(1.2 < Y < 7) if Y ∼ N(3, 4
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1193109: P(x<69.1)=
Answer by ikleyn(52786)   (Show Source): (Show Source):
Question 1189095: A soft drink machine is regulated so that it discharges an average of 200 milliliters per cup. If the
amount of drink is normally distributed with a standard deviation equal to 15 millimeters, a) what fraction of the cups will contain more than 240 milliliters?
b) c) what is the probability that a cup contains between 191 and 209 milliliters? how many cups will likely overflow if 230 milliliters cups are used for the next 1000 di
d)
below what value do we get the smallest 25% of the drinks?
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! z(240)>(240-200/15 or +2.67
probability z> 2.67=0.0038
-
between 191 and 209 is the same way.
calculator 2ndVARS(191,209,200,15) and that will equal twice the probability of z=9/15 or -.6
=0.4515.
-
230 ml cups are two sd over or 0.02275 probability, so 22.75 or 23 cups would be expected to overflow
-
z(0.25)=-0.6745=(x-200)/15
-10.12=x-200
x=189.88 or 190 ml
Note: there is an error in the problem. The SD is 15 milliliters. All units are in ml.
Question 1188811: a school with 60 teachers is on alert during a nighttime
storm
to inform teachers whether the school will open the next day , the princeipal will call four teachers
each of whom will then call 2 others
and each of these will again call 2 others
so on untill all 60 have been contacted
how many people have to make 2 calls?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To solve the problem, I prepared this Table below
T A B L E
step how many how mamy
# teachers know teachers don't know
1 a principal 4 60 - 4 = 56
calls to 4 teachers
2 4 teachers call
to 8 other teachers 4 + 8 = 12 56 - 8 = 48
3 8 teachers calls
to 16 other teachers 12 + 16 = 28 48 - 16 = 32
4 16 teacher calls
to 32 other teachers 28 + 32 = 60 32 - 32 = 0
Now from the table, the number of people (= of teachers) who made 2 calls is 4 + 8 + 16 = 28.
ANSWER. The number of people who made 2 calls is 28.
Solved.
/////////////
Now, as you see this solution and this table, you can, probably, organize
your arguments in other, more compact form to produce your own solution.
Question 1186477: The waiting times between a subway departure schedule and the arrival of a passenger are uniformly distributed between 0 and 5 minutes. Fine the probability that a randomly selected passenger had a waiting time less than 2.75 minutes.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1185582: 2. The medical Rehabilitation Education Foundation reports that the average cost of rehabilitation forstroke victims is $24,672. To see if the average cost of rehab is different at a particular hospital, a researcher selects a random sample of 35 stroke victims at the hospital and find the average cost of their rehab is $25,250. The standard deviation of the population is $3,251. At α= 0.01, can it be concluded that the average cost of stroke rehabilitation at the particular hospital is different from $24,672?a) State thenull and alternativehypotheses.b) Find the critical value from the appropriate table.c) Compute the test value.d) Make the decision to reject or not reject the null hypothesis.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! population average cost of rehabilitation is 24672.
population standard deviation is 3251.
sample size is 35
sample mean is 25250
standard error = standard deviation / square root of sample size = 3251 / sqrt(35) = 549.5193 rounded to 4 decimal places.
sample size is over 30 and population standard deviation is known.
use of z-score is indicated.
here's a guideline on when to use the z-score versus when to use the t-score.
https://math.stackexchange.com/questions/1817980/how-to-know-when-to-use-t-value-or-z-value
use the z-score formula to find the z-score.
the formula is:
z = (x - m) / s
z is the z-score
x is the mean of the sample
m is the mean of the population
s is the standard error
the formula becomes:
z = (25250 - 24672) / 549.5193 = 1.05 rounded to 2 decimal places.
since you want to find out if the mean of the sample is significantly different from the mean of the population, you will use a two-tail significance level.
the two-tail significance level is .01/2 = .005.
the two-tail confidence interval is equal to .99.
the significance level is the tail that is equal to .01 divided between the lower and upper limit of the confidence interval.
that makes is .005 above and .005 below.
the critical z-score would be plus or minus 2.5758.
this was found using the z-score calculator at https://davidmlane.com/hyperstat/z_table.html
a display of the results of using that calculator is shown below.

the area was entered as .01 with the results of finding the z-score that had half of that above the confidence interval and half below.
since the absolute value of the test z-score is significantly less than the absolute value of the critical z-scores, the results of the test are not significant, indicating there is not enough evidence to say that the mean at the hospital is different than the mean at the general population of all hospitals.
Question 1184449: please help me with this question, it would be highly appreciated:
3 tiles with the letter X on them and 3 tiles with the letter O on them are placed in a row. The order is chosen at random. What is the probability that no two adjacent tiles have the same letter on them?
Thank you taking time out of your day to help me!
Found 2 solutions by robertb, ikleyn:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of ways of lining up 6 objects 3 of which are identical and the other 3 also identical (but different from the previous three) is
 . (You can even list these arrangements!) . (You can even list these arrangements!)
Now two such arrangements which satisfy the condition are XOXOXO and OXOXOX.
The movement of even one letter in either arrangement into another spot will produce
an arrangement where two adjacent tiles have the same letter on them. This resulting arrangement will belong to the other 18 arrangements.
In other words XOXOXO and OXOXOX uniquely satisfy the condition of the problem.
Therefore the probability that no two adjacent tiles have the same letter on them is 2/20, or 1/10.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me with this question, it would be highly appreciated:
3 tiles with the letter X on them and 3 tiles with the letter O on them are placed in a row.
The order is chosen at random. What is the probability that no two adjacent tiles have the same letter on them?
Thank you taking time out of your day to help me!
~~~~~~~~~~~~~~~~
One such base configuration is XOXOXO,
with 3! = 6 permutations of X's and 3! = 6 permutations of O's; in all 6*6 = 36 possible permutations inside this configuration.
Similarly, there are 36 possible permutations inside the other base configuration OXOXOX.
In all, there are 36 + 36 = 2*36 = 72 favorable permutations among 6! = 6*5^4*3*2*1 = 720 all possible permutations of 6 letters.
In terms of probability, it is P = 72/720 = 0.1 to have a preferable configuration, randomly.
Solved and explained.
Question 1183741: For each of the following tobs values, determine the highest level of
significance associated with the decision taken.5
tobs df Decision
(i) 4.000 17 Reject Ha for a two-tailed test
(ii) 1.200 120 Reject Ha for a one-tailed test
(iii) -2.660 16 Reject Ha for both one-tailed
and two-tailed test
(iv) -1.586 60 Reject Ha for a one-tailed test
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1183581: From actual road tests with the tires, Hankook Tires estimated that the mean tire mileage is 36,500 miles and that the standard deviation is 5000 miles. Data is normally distributed.
(i) What percentage of the tires can be expected to last more than 40,000 miles?
(ii) Assume that Hankook Tires is considering a guarantee that will provide a discount on replacement tires if the original tires do not provide the guaranteed mileage. What should the guarantee mileage be if the company wants no more than 10% of the tires to be eligible for the discount guarantee?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From actual road tests with the tires, Hankook Tires estimated that the mean tire mileage is 36,500 miles
and that the standard deviation is 5000 miles. Data is normally distributed.
(i) What percentage of the tires can be expected to last more than 40,000 miles?
(ii) Assume that Hankook Tires is considering a guarantee that will provide a discount on replacement tires
if the original tires do not provide the guaranteed mileage. What should the guarantee mileage be
if the company wants no more than 10% of the tires to be eligible for the discount guarantee?
~~~~~~~~~~~~~~~~
I think that the basic assumption made in this problem that the tire mileage is described by the normal distribution
is INCORRECT and CONTRADICTS to COMMON SENSE, as well as to the MATERIAL SCIENCE.
THEREFORE, I think, the problem, as it is worded, printed, posted and presented, is a FAKE.
/////////////
It is the same as to assume that the age of people is distributed normally, which is, OBVIOUSLY, not a case.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the mean is 36500.
the standard deviation is 5000.
z = (x - m) / s
z is the z-score
x is the raw score
m is the raw mean
s is the standard deviation.
z = (40000 - 36500) / 5000 = .7
the area to the left of a z-score of .7 is equal to .7580364218.
round to 4 decimal places to get .7580.
.7580 * 100 = 75.8% of the tires will not last more than 40000 miles.
that means that 100% - 75.8% = 24.2% will last more than 40000 miles.
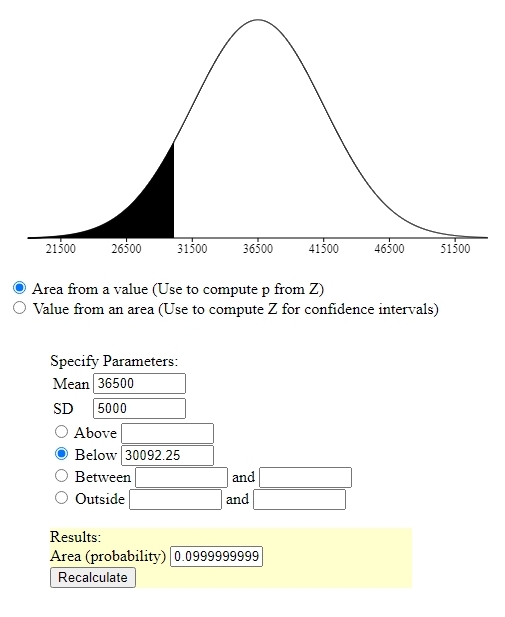
for 10% of the tires not to last more than the guaranteed mileage, the guaranteed mileage needs to have a z-score of
if they guarantee the tires to last more than 42907.75 miles, then they will only have to provide a discount for 10% of the tires.
the required z-score will be equal to -1.28155 rounded to 5 decimal places.
use the z-score formula to find the raw score.
z = (x - 36500) / 5000 becomes -1.28155 = (x - 36500) / 5000.
solve for x to get x = -1.28155 * 5000 + 36500 = 30092.25.
if they guarantee the tires to last at least 30092.25 miles, then they will only have to provide a discount for 10% of the tires.
these results can be seen in the following displays.
the first display shows the ratio of tires not lasting more than 40000 miles.
the second display shows the percent tires that will not last more than 42909.4 miles.

Question 1182887: The percentage of the adult population in a large city that are women is 45%.
A court is to randomly select a jury of adults from the population of all adults in
this city. Find the probability that none of the 12 randomly selected adults
from this city is a woman.
1. Determine the binomial parameters, n and p, giving values and descriptions.
2. Determine the question being asked, P(x “=, <, <, >, or >” a number), that is, write the
question symbolically as illustrated in lecture videos (and page 2 of this lab 3 packet).
3. Determine the calculator command needed to solve the problem.
(See separate sheet on using calculator to solve binomial problems.)
4. Use the calculator to find the solution to the binomial probability;
round answers to 4 decimal places.
5. Write your answer in a sentence in terms of the application
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Cutting and pasting your entire assignment, with nothing else in your post, does a couple of things....
(1) It strongly suggests you simply want us to do your work for you -- which is not the purpose of this forum.
(2) It tells us you aren't even putting in any effort to make the post usable to us; we don't have access to your lecture videos, lab packets, or the sheet on using a calculator to solve binomial probability problems.
Question 1181387: Doris is ranked at the first quartile in her senior class of 300 students. What is her rank in the class?
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! can do (n+1)/4=75.25 so she is 75th.
or the median is between the 150th and 151st.
The first quartile is the median of the lower half, and that has 150 members, so she is 75th.
Question 1179759: In Statistics and Probability examination, the average grade was 74 and the standard deviation was 7. If 11.9% of the class is given X’s scores, and the grades follow a normal distribution, what is the lowest possible score X and the highest possible score Y?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Normal Distribution: µ = 74 and σ = 7
11.9% of the class is given X’s score
.0595 above and below the mean: .5 + .0595 = .5595
invNorm(.5595,74,7) = 75
the highest possible score X is 75 (1 to the right of mean 74)
lowest is 74 - 1 = 73
Your Reference did not work for me.
If the intent was for 11.9% to get As...
invNorm(.881,74,7) = 82.26 Round Up to next whole number
or
  7*1.18 + 74 = 82.26 Round Up to next whole number
For As: lowest is 83 and highest, would be a possible 100.
Wish You the Best in your Studies.
7*1.18 + 74 = 82.26 Round Up to next whole number
For As: lowest is 83 and highest, would be a possible 100.
Wish You the Best in your Studies.
Question 1179519: A man gets a raise of 12% in salary at end of first year and further raises of 16% ,19% and 25% at the end of second, third and fourth years respectively; the raise in each year being calculated on his salary at the beginning of the year. What is the average annual percentage increase?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
@greenestamps correctly noticed that this problem formulation admits SEVERAL different interpretations.
I came with my own interpretation and with my own solution.
After the 1st year, the salary is 1.12 of the original salary.
After the 2nd year, the salary is 1.16*1.12 of the original salary.
After the 3rd year, the salary is 1.19*1.16*1.12 of the original salary.
After the 4th year, the salary is 1.25*1.19*1.16*1.12 of the original salary.
So, after 4 years, the salary is 1.25*1.19*1.16*1.12 = 1.93256 of the original salary.
They want you to find an EQUIVALENT annual growth coefficient that provides this calculated increase of salary in four years.
For it, you should solve this equation
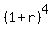 = 1.93256.
It is easy to do:
1 + r = = 1.93256.
It is easy to do:
1 + r =  = 1.179 (rounded).
It gives then average annual percentage increase r = 1.179 - 1 = 0.179, or 17.9%. ANSWER = 1.179 (rounded).
It gives then average annual percentage increase r = 1.179 - 1 = 0.179, or 17.9%. ANSWER
Solved, with my interpretation N 3.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1179065: At a local high school, GPA's are normally distributed with a mean of 2.9 and standard deviation of 0.6. What is the GPA of the highest 2.5% of the students?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
GPA's are normally distributed: µ = 2.9 and σ = .6
the GPA of the highest 2.5% of the students:
invNorm(.025) = 1.96
 , ,  1.96*(.6) + 2.9 = 4.1
Wish You the Best in your Studies.
1.96*(.6) + 2.9 = 4.1
Wish You the Best in your Studies.
Question 1178343: The weights of a certain group of high school boys have a normal distribution with a mean of 146 lb and a standard deviation of 10lb. Find the percent of the group having a weight
(a) greater than 154 lb.
(b) less than 132 lb.
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! z=(x-mean)/sd
> 154 is z > (154-146)/10 or z> 0.8. Has probability 0.2119 or 21.2%
-
< 132 is z < (132-146)/10 or -1.4. Has probability of 0.0808 or 8.1%
Question 1177853: If a golfer tees off 50 times on 10,000 square foot course how many times (what is the probability) that he will land on the 1,200 foot green that lies within that 10,000 foot course. :a probability & area question
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If I understand the problem's meaning correctly from the context,
the probability the problem asks for is the ratio P = 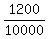 = =  = 0.12 = 12%. ANSWER = 0.12 = 12%. ANSWER
Question 1177087: In a survey of 250 Voters prior to the election, 16% indicated that they would vote for the ABC candidate. Estimate with 90% confidence the population proportion of voters who support the ABC.
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! the half-interval is z(0.95)*sqrt(p*(1-p)/n)
=1.645*sqrt(.16*.84/250)
=0.038
The interval is (0.122, 0.198), equidistant from the point estimate of 16%
A tree diagram would be very difficult with 250 voters.
Question 1174777: Among 200 patients at a Tikur Anbessa hospital.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One and ONLY ONE problem/question per post.
It is the RULE, the POLICY and the REQUIREMENT of this forum.
It is written in this page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
Question 1174512: In a certain communications system, there is an average of 1 transmission error per 10 seconds Let the distribution of transmission errors, say X be a Poisson distribution. What is the probe ability of more than 1 error in a communication half minute in duration?
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! The errors are proportional to time, so would expect the half-minute distribution to be Poisson with lambda=3.
probability of 0 and 1 are
p(0)=e^(-3)^3^0/0!=0.0498
p(1)=e^(-3)*3^1/1!=0.1494
that sum is 0.1992
the probability of more than 1 is the complement or 0.8008
Question 1173518: Find the z-score that corresponds to the following areas.
Area to the left is 1.24
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! with normal distributions, the total area is 1 and anything else has to be between 0 and 1.
if we assume you are talking in percents, then the total area is 100% and 1.24% / 100% would be equal to .0124.
the z-score with an area of .0124 to the left of it would be equal to -2.244503871.
round this to 3 decimal places and it becomes -2.245.
i used my ti-84 plus scientific calculator to get the more detailed answer.
the tables and the calculators assume that the area is a ratio of the area to the left of the z-score divided by the whole area under the normal distribution curve.
the whole area under the normal distribution curve is assumed to be equal to 1.
that's why they show the area to the left of a z-score as a ratio between 0 and 1.
here's a reference on z-score tables and how to find the area to the left of the z-score.
https://mathbitsnotebook.com/Algebra2/Statistics/STzScores.html#:~:text=To%20find%20a%20specific%20area,on%20a%20standard%20normal%20distribution.&text=You%20need%20both%20tables!
most tables are full tables, so concentrate on that.
the table i normally reference can be found at https://www.math.arizona.edu/~rsims/ma464/standardnormaltable.pdf
using that table, i found that the z-score of -2.24 gave an area of .01255 to the left of it and the z-score of -2.25 gave an area of .01222 to the left of it.
.0124 was in between z-score of -2.24 and -2.25.
i manually interpolated to get a z-score of -2.2445 which is equal to -2.245 when rounded to 3 decimal places.
whether i used my ti-84 plus calculator, or used the table and manually interpolated, i got a z-score of -2.245 rounded to 3 decimal places.
that's usually close enough.
a calculator you can use online can be found at https://stattrek.com/online-calculator/normal.aspx
using that calculator, i got a z-score of -2.245 with a lot less work than manual interpolation.
Question 1172896: A phone company keeps statistics on the number of messages text that your customers send each month. According to statistics, the number of messages sent per customer in a month has a normal distribution. The data is shown below.
• The average is 278 messages per month.
• The standard deviation is 19 messages per month.
What is the probability that a customer sends LESS than 316 messages in a month?
Answer by Boreal(15235)   (Show Source): (Show Source):
Question 1172478: The heights of applicants to the police force are normally distributed with mean 170 cm and standard deviation 3.8 cm. If 30% applicants are rejected on account of their low height. What is the minimum acceptable height for the police force?�
Answer by Boreal(15235)   (Show Source): (Show Source):
|
|