Question 1150793: Pls, I Need Ur Help In This Question, With Full Explaination.
Find the equations whose perpendicular distance is of length 3 units and at 60(degree) from the x-axis.
Found 2 solutions by Theo, Alan3354:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you're talking about the equation of a straight line, then i believe your answer will be y = sqrt(3) * x
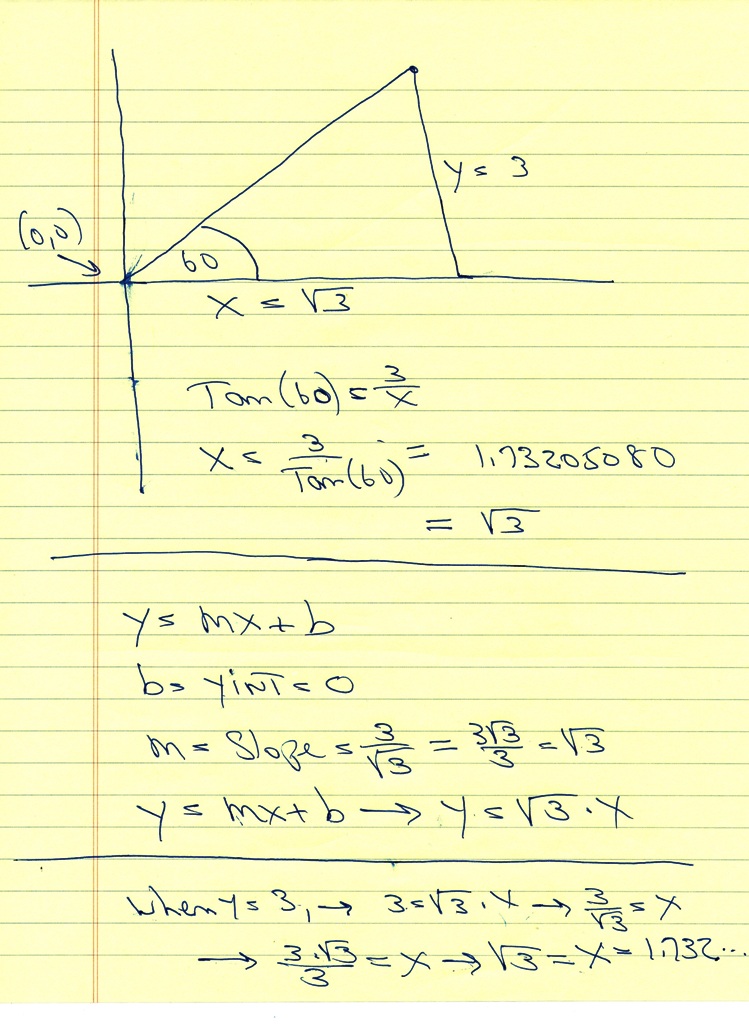
you form a triangle with the vertex of the angle at the point (0,0).
the angle is 60 degrees.
your y-value is the height of the triangle.
your x-value is the distance from the y-axis to the point where y = 3.
your equation is tan(60) = y / x.
when y = 3, the equation becomes tan(60) = 3/x
solve for x to get x = 3 / tan(60) = 1.732050808.
this this the same as x = sqrt(3).
therefore, you have 2 points on the line.
they are (0,0) and (sqrt(3),3).
the slope intercept form of the equation of a straight line is y = mx + b.
m is the slope and b is the y-intercept.
when x = 0, y = 0 because that's the vertex of the angle formed so.
your y-intercept is therefore equal to 0 and the equation becomes y = mx + 0 which becomes y = mx.
the slope is equal to (y2 - y1) / (x2 - x1)
(x1,y1) = 0,0)
(x2,y2) = (sqrt(3),3)
(y2 - y1) / (x2 - x1) becomes (3 - 0) / (sqrt(3) - 0) = 3 / sqrt(3).
3 / sqrt(3) * sqrt(3) / sqrt(3) = 3 * sqrt(3) / 3 = sqrt(3).
your slope is sqrt(3).
your equation of the straight line becomes y = sqrt(3) * x.
when y = 3, solve for x to get x = 3 / sqrt(3) = 3 * sqrt(3) / 3 = sqrt(3) = 1.732050808 which rounds to 1.732 as shown on the graph.
here's my worksheet.
the top point on the right of the triangle is the point (sqrt(3), 3).
here's the graph of the equation of y = sqrt(3) * x.
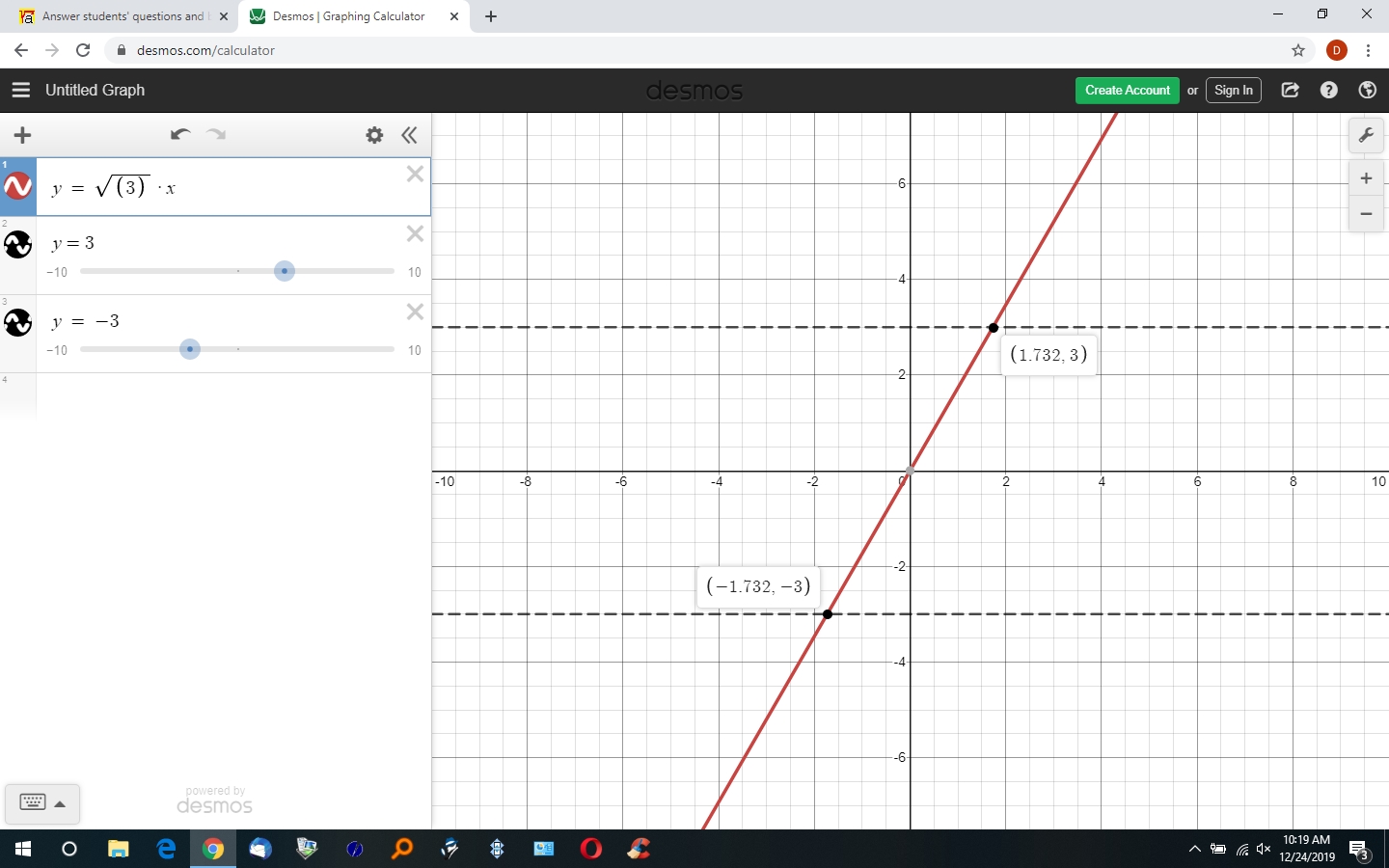
i think your solution is that the equation of the line is y = sqrt(3) * x.
the domain is all real values of x.
the range is all real values of y.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equations whose perpendicular distance is of length 3 units and at 60(degree) from the x-axis.
================
A perpendicular distance of 3 units implies it's parallel to the x-axis. If it's not parallel, the distance varies.
No solution.
|
|
|