|
This Lesson (STATSTICS FROM A FREQUENCY OR PROBABILITY DISTRIBUTION) was created by by Theo(13342)
  About Theo:
a frequency distribution is a set of numbers where each distinct number is shown once with the number of occurrences of that number being displayed as well.
a probability distribution is a set of numbers where each distinct number is shown once with the probability of the occurrence of that number being displayed as well. they are related in that the probability distribution can be calculated from the frequency distribution and vice versa. as an example: if your data set contains 1,1,1,2,2,3,3,3,3,3, then your frequency distribution would look like this:
number frequency number * frequency
1 3 3
2 2 4
3 5 15
total n/a 10 22
the total for number is n/a because it's not applicable to the problem. the sum of your frequency is 10. the sum of your number * frequency is 22. the average is equal to the sum of your number * frequency divided by the sum of your frequency, which is equal to 22 / 10 which is equal to 2.2 the probability of the number 3 occurring in your data set is 3/10. the probability of the number 2 occurring in your data set is 2/10. the probability of the number 3 occurring in your data set is 5/10. your probability distribution for the same data set would look like this:
number probability number * frequency
1 3/10 3/10
2 1/10 4/10
3 5/10 15/10
total n/a 1 22/10
the sum of your probability is 1. the sum of your number * probability is 22/10 the average is equal to the sum of your number * probability divided by the sum of your probability, which is equal to (22 / 10) / 1 which is equal to 22 / 10 which is equal to 2.2. you get the same answer whether or not you use the frequency distribution of the probability distribution. as you will see below, you will get the same answer for average, variance, and standard deviation whether or not you use a frequency distribution or a probability distribution. the following table shows the method used to find the mean, sum of squares, variance, and standard deviation of a frequency distribution. 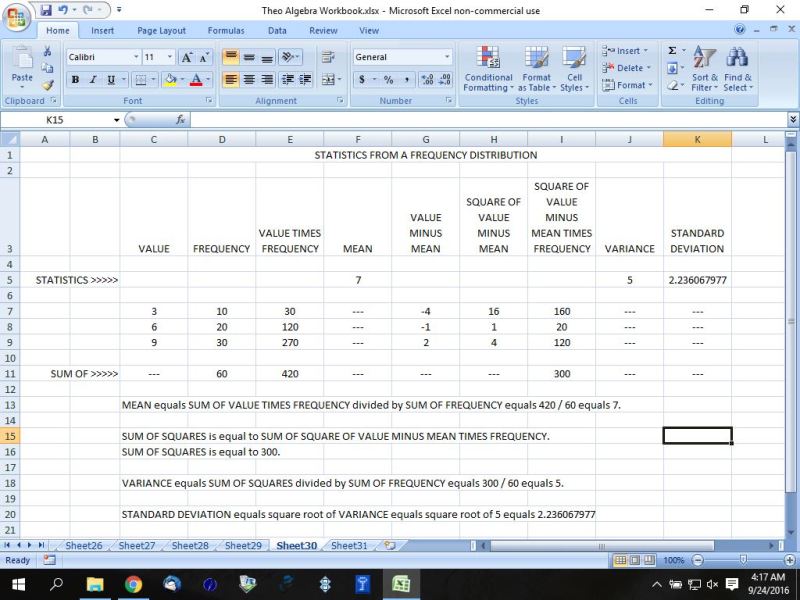
the following table shows the method used to find the mean, sum of squares, variance, and standard deviation of a probability distribution. 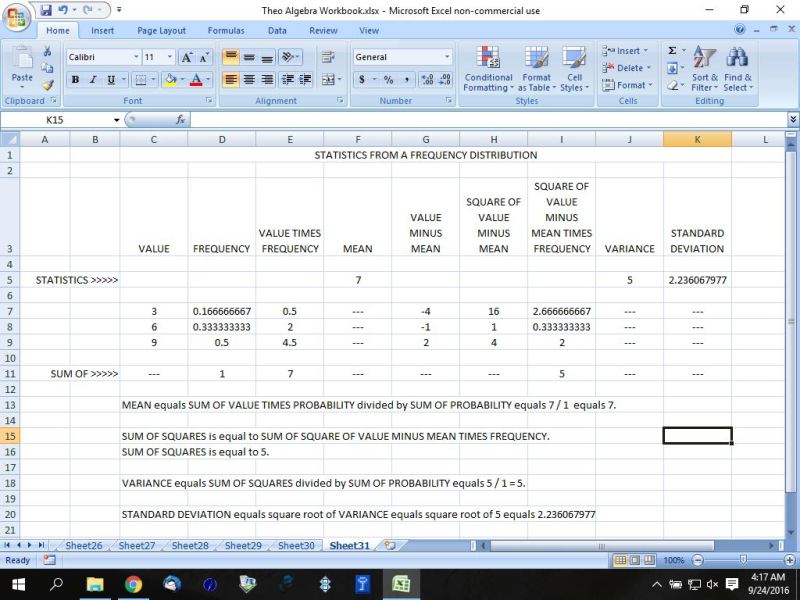
these two tables are connected in that the underlying data is the same. the only difference is that the first table uses frequency of occurrence while the second table uses probability of occurrence. since probability of occurrence is derived from frequency of occurrence, and vice versa, it stands to reason that the statistics generated will be the same. the formula to convert frequency of occurrence (shown as FREQUENCY) to probability of occurrence (shown as PROBABILITY) is as follows. probability of occurrence equals frequency of occurrence divided by sum of frequency of occurrence. for example, in the first table, the number 3 occurs in the data set 10 times. that is why its frequency is shown as 10. the sum of all the frequencies is equal to 60. this is equivalent to telling you that there are 60 data elements in the data set. 10 of them are the number 3 20 of them are the number 6 30 of them are the number 9 the probability of the number 3 occurring in the data set is therefore 10/60 = 1/6. the decimal equivalent of 1/6 is equal to .166666..... which is shown in the excel spreadsheet as 0.166666667. the probability of the number 6 occurring in the data set is therefore 20/60 = 2/6 = 1/3. the decimal equivalent of 1/3 is equal to .33333..... which is shown in the excel spreadsheet as .333333333. the probability of the number 9 occurring in the data set is therefore 30/60 = 3/6 = 1/2. the decimal equivalent of 1/2 is equal to .5 which is shown in the excel spreadsheet as .5. the sum of all probabilities is equal to 1/6 + 1/3 + 1/2 which is equal to 1/6 + 2/6 + 3/6 which is equal to 1. in statistics, the sum of all probabilities must always equal to 1, so if it's not, then you did something wrong. the bottom line is that, whether you use a frequency distribution or a probability distribution, the same method applies to both and can be used inter-changeably. in the spreadsheet, there is a row that is called STATISTICS >>>>>. this row contains the MEAN and the VARIANCE and the STANDARD DEVIATION in the appropriate column. in the spreadsheet, there is another row that is called SUM OF >>>>>. this row contains the sum of whatever is contains in the appropriate column. for example: SUM OF SQUARE OF VALUE MINUS MEAN TIMES FREQUENCY is the sum of all the values contains in the column titled SQUARE OF VALUE MINUS MEAN TIMES FREQUENCY. in the frequency distribution, that value would be 300. in the probability distribution, that value would be 5. in statistics, the SUM OF SQUARE OF VALUE MINUS MEAN TIMES FREQUENCY is called SUM OF SQUARES. if you have any questions regarding this, or require further clarification, send an email to dtheophilis@gmail.com. This lesson has been accessed 2895 times. |