A researcher wants to estimate with 99% confidence, the proportion of people who have a computer desktop. A previous study showed that 30% of those interviewed had a computer desktop at home. The researcher wants to be accurate within 3% of the true proportion. What is the minimum sample size to be needed?
See Probability-and-statistics/1060911 below.
Do it the same way. You only need a) though.
Pay attention to the different values. For example, in yours, Margin of Error (E) is: 3% (.03) instead of 5% (.05).
A researcher wishes to estimate the proportion of adults who have high-speed Internet access. What size sample should be obtained if she wishes the estimate to be within 0.05 with 99% confidence if
(a) she uses a previous estimate of 0.36?
(b) she does not use any prior estimates?
The ESTIMATED SAMPLE PROPORTION should be calculated using the following formula: n = p̂q̂
(a)
Now, with a PRELIMINARY ESTIMATE of .36, p̂ = .36, and q̂ = 1 - p̂ = 1 - .36 = .64
Since this is a 99% CONFIDENCE INTERVAL, then significance level is 
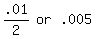, and so, 
E (Margin of Error) = .05
Therefore, n = p̂q̂ becomes: 
(b)
Now, since NO PRELIMINARY ESTIMATE WAS GIVEN/WAS AVAILABLE, then .5(50%) should be used for p̂, or for the ASSUMED proportion
With p̂ being .5, q̂ = 1 - p̂ = 1 - .5 = .5
Since this is a 99% CONFIDENCE INTERVAL, then significance level is 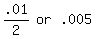, and so,
E (Margin of Error) = .05
Therefore, n = p̂q̂ becomes: 
When I used STATDISK to calculate the ESTIMATED SAMPLE PROPORTION, I got the same result: a) 612 and b) 664 adults.
This problem looks a lot like one from Chamberlain College of Nursing. I tutor a lot of nursing students who attend that college. Is that where you attend?
