SOLUTION: You are taking a true/false test that has 60 questions If you guess on each question, and have the same chance of guessing the correct answer on each question, what is the probabi

The original problem is a binomial distribution probability problem.
The number of trials is n= 60;  the probability of success is p= 1/2 = 0.5 
for each individual trial.


Since the number of trials is great, the method of solution is to use a normal
distribution approximation.
 


About approximation of the binomial distribution by normal distribution and continuity correction factor 
see your textbook and/or these Internet sources

https://www.statology.org/normal-approximation

https://www.statisticshowto.com/probability-and-statistics/binomial-theorem/normal-approximation-to-the-binomial/

https://online.stat.psu.edu/stat414/lesson/28/28.1

https://stats.libretexts.org/Courses/Las_Positas_College/Math_40%3A_Statistics_and_Probability/06%3A_Continuous_Random_Variables_and_the_Normal_Distribution/6.04%3A_Normal_Approximation_to_the_Binomial_Distribution



For this normal distribution approximation, the mean value is m = n*p = 0.5*60 = 30;
the standard deviation is 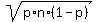 =  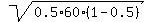= 3.87298 (rounded).


Next, at least 65% of 60 questions is at least  = 39 questions to answer correctly.


Therefore, to answer the problem's question, you should find the area under the the described 
normal curve on the RIGHT of the raw mark 38.5 (we use the continuity correction factor).


So, if you use a regular calculator TI-83 or TI-84, you can get the answer using 
the standard normalcdf function

                       z1     z2    mean     SD      <<<---===  formatting pattern
        P = normalcdf(38.5, -9999,   30,  3.87298).


You get the value of 0.014  (rounded).      ANSWER