SOLUTION: Licensed Drivers in the Unites States In a recent year there were the following numbers (in thousands) of licensed drivers in the United States. (2+3+3=8 pts) MALE FEMALE Age 19

Click here to see ALL problems on Binomial-probability

Question 1178706: Licensed Drivers in the Unites States In a recent year there were the following
numbers (in thousands) of licensed drivers in the United States. (2+3+3=8 pts)
MALE FEMALE
Age 19 and under 4746 4517
Age 20 1625 1553
Age 21 1679 1627
Choose one driver at random. Find the probability that the driver is
a. Male Age 19 years and under. Answer:-
b. Age 20 or female Answer:-
c. At least 20 years old Answer:-
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website!
.

Licensed Drivers in the Unites States In a recent year there were the following numbers (in thousands) of licensed drivers in the United States. (2+3+3=8 pts) MALE FEMALE Age 19 and under 4746 4517 Age 20 1625 1553 Age 21 1679 1627 Choose one driver at random. Find the probability that the driver is a. Male Age 19 years and under. b. Age 20 or female c. At least 20 years old
~~~~~~~~~~~~~~~

            This problem is SPECIAL.
            It is special, because you do not need to think to solve it.
            You simply write formulas as you read the text.

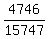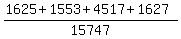First, calculate the total number of people in the table 4746 + 4517 + 1625 + 1553 + 1679 + 1627 = 15747. Now (a) P = . Use your calculator. (b) P = . Use your calculator. (c) P = 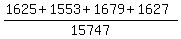. Use your calculator.

The formulas are self-explanatory.

You even do not need to know a formal definition of what the probability is.

The common sense and a bit of intuition at the level of advanced kindergarten alumni is enough
to solve this problem to the end without any help from outside.