Question 1166570: According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. You randomly select six peanut M&M’s from an extra-large bag of the candies. (Round all probabilities below to four decimal places; i.e. your answer should look like 0.1234, not 0.1234444 or 12.34%.)
Compute the probability that exactly three of the six M&M’s are blue.
Compute the probability that three or four of the six M&M’s are blue.
Compute the probability that at most three of the six M&M’s are blue.
Compute the probability that at least three of the six M&M’s are blue.
If you repeatedly select random samples of six peanut M&M’s, on average how many do you expect to be blue? (Round your answer to two decimal places.)
blue M&M’s
With what standard deviation? (Round your answer to two decimal places.)
Answer by ikleyn(53553)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow,
12% are red, 23% are blue, 23% are orange and 15% are green. You randomly select six peanut M&M’s
from an extra-large bag of the candies. (Round all probabilities below to four decimal places;
i.e. your answer should look like 0.1234, not 0.1234444 or 12.34%.)
(a) Compute the probability that exactly three of the six M&M’s are blue.
(b) Compute the probability that three or four of the six M&M’s are blue.
(c) Compute the probability that at most three of the six M&M’s are blue.
(d) Compute the probability that at least three of the six M&M’s are blue.
(e) If you repeatedly select random samples of six peanut M&M’s, on average how many do you expect to be blue?
(Round your answer to two decimal places.)
(f) With what standard deviation? (Round your answer to two decimal places.)
~~~~~~~~~~~~~~~~~~~~~~~~~
(a) In this case, we have a binomial distribution with n=6 trials, k=3 successful trials.
p=0.23 probability of the individual success in each trial. Apply the standard formula for this probability
P = 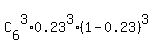 = = 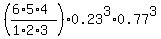 = 0.1111 (rounded). ANSWER
(b) In this case
P = P(3) + P(4) = = 0.1111 (rounded). ANSWER
(b) In this case
P = P(3) + P(4) = 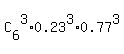 + + 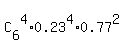 =
= =
= 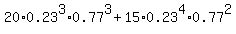 = 0.1360 (rounded). ANSWER
(c) Continue in the same style
P = P(0) + P(1) + P(2) + P(3) = . . . = 0.972 (rounded). ANSWER
To replace monotonic calculations, you may use very convenient online calculator
https://stattrek.com/online-calculator/binomial/
(d) Continue in the same style
P = P(3) + P(4) + P(5) + P(6) = 1 - ( P(0) + P(1) + P(2) ) = 1 - 0.8609 = 0.1391 (rounded). ANSWER
To replace monotonic calculations, you may use very convenient online calculator
https://stattrek.com/online-calculator/binomial/
(e) Mathematical expectation is n*p = 6*0.23 = 1.38 blue peanuts.
(f) With the standard deviation SD = = 0.1360 (rounded). ANSWER
(c) Continue in the same style
P = P(0) + P(1) + P(2) + P(3) = . . . = 0.972 (rounded). ANSWER
To replace monotonic calculations, you may use very convenient online calculator
https://stattrek.com/online-calculator/binomial/
(d) Continue in the same style
P = P(3) + P(4) + P(5) + P(6) = 1 - ( P(0) + P(1) + P(2) ) = 1 - 0.8609 = 0.1391 (rounded). ANSWER
To replace monotonic calculations, you may use very convenient online calculator
https://stattrek.com/online-calculator/binomial/
(e) Mathematical expectation is n*p = 6*0.23 = 1.38 blue peanuts.
(f) With the standard deviation SD = 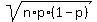 = = 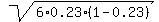 = 1.0308 (rounded). ANSWER = 1.0308 (rounded). ANSWER
Solved: all questions are answered.
|
|
|