.
The binomial expansion is this formula
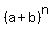 =
=  +
+ 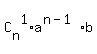 +
+ 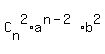 +
+ 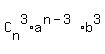 + . . . +
+ . . . + 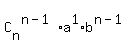 +
+ 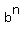 (see this Wikipedia article https://en.wikipedia.org/wiki/Binomial_theorem or my lesson
Binomial Theorem, Binomial Formula, Binomial Coefficients and Binomial Expansion in this site).
For our case, the term containing
(see this Wikipedia article https://en.wikipedia.org/wiki/Binomial_theorem or my lesson
Binomial Theorem, Binomial Formula, Binomial Coefficients and Binomial Expansion in this site).
For our case, the term containing 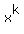 is
is 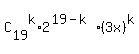 , while the term containing
, while the term containing 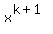 is
is 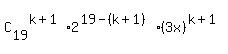 ,
and they want to know at which k the coefficients at
,
and they want to know at which k the coefficients at 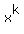 and
and 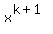 are the same:
are the same:
 =
= 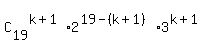 . (1)
(notice the difference between "the terms" and "the coefficients" !)
From (1), you have
. (1)
(notice the difference between "the terms" and "the coefficients" !)
From (1), you have
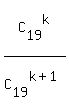 =
=  , or, simplifying the right side,
, or, simplifying the right side, 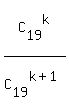 =
=  . (2)
Next, use
. (2)
Next, use 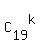 =
= 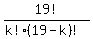 ,
, 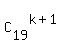 =
= 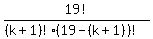 .
Substitute it into the left side fraction of (2), and you will get after canceling common factors
.
Substitute it into the left side fraction of (2), and you will get after canceling common factors
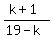 =
=  ,
2*(k+1) = 3*(19-k) ====> 2k + 2 = 57 - 3k ====> 2k + 3k = 57 - 2 ====> 5k = 55 ====> k =
,
2*(k+1) = 3*(19-k) ====> 2k + 2 = 57 - 3k ====> 2k + 3k = 57 - 2 ====> 5k = 55 ====> k = 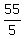 = 11.
Answer. k = 11.
= 11.
Answer. k = 11.