.
1. 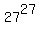 =
= 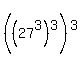 .
Let us go up on this upstairs from the bottom to the top step by step.
2. First consider the number
.
Let us go up on this upstairs from the bottom to the top step by step.
2. First consider the number 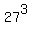 . It is 19683:
. It is 19683:
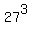 = 19683.
Write it in the form
= 19683.
Write it in the form 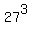 =
= 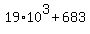 .
It is clear that for
.
It is clear that for 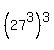 and for
and for 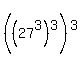 the last three digits are determined by last
three digits "683" of the number
the last three digits are determined by last
three digits "683" of the number 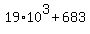 .
The part
.
The part 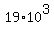 does not affect the last three digits of the number
does not affect the last three digits of the number 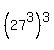 .
It is exactly what the binomial theorem says and provides in this situation.
Therefore, in finding the three last digits of the number
.
It is exactly what the binomial theorem says and provides in this situation.
Therefore, in finding the three last digits of the number 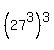 we can track only for
we can track only for 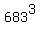 and do not concern about other terms.
It implies that the last three digits of the number
and do not concern about other terms.
It implies that the last three digits of the number 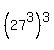 are exactly the same as the last three digits of the number
are exactly the same as the last three digits of the number 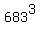 .
The number
.
The number 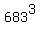 = 318611987, as easy to calculate (I used Excel in my computer), so its last three digits are 987.
3. Now we can make the next (and the last) step up on this upstairs in the same way.
The last three digits of the number
= 318611987, as easy to calculate (I used Excel in my computer), so its last three digits are 987.
3. Now we can make the next (and the last) step up on this upstairs in the same way.
The last three digits of the number 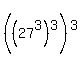 are the same as the last three digits of the number
are the same as the last three digits of the number 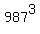 , and it is easy to calculate.
, and it is easy to calculate.
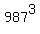 = 961504803, and its last three digits are 803.
Therefore, the last three digits of the number
= 961504803, and its last three digits are 803.
Therefore, the last three digits of the number 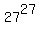 are 803.
are 803.
Solved.