Can someone help me to solve this?
When (1-3x)^n is expanded, the coefficient of x^2 is 90. How to find n algebraically?
This is saying that there’s a specific term that’s 90x2
The formula to find a SPECIFIC term in a BINOMIAL expansion is:
 , where r = term number
, where r = term number
 ------ Substituting 1 for a, and - 3x for b
------ Substituting 1 for a, and - 3x for b
 ------- Replacing
------- Replacing 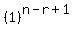 with 1 as 1 raised to ANY POWER equals 1
with 1 as 1 raised to ANY POWER equals 1
 From this, we can see that:
From this, we can see that:  Therefore, r – 1 MUST = 2
r, or term number with the term 90x2 = 2 + 1 = 3
Since r = 3, then
Therefore, r – 1 MUST = 2
r, or term number with the term 90x2 = 2 + 1 = 3
Since r = 3, then  becomes:
becomes:






 ------- Cross-multiplying
n(n – 1) = 20
Observing the above equation, it's clear that:
------- Cross-multiplying
n(n – 1) = 20
Observing the above equation, it's clear that:  , as 5(5 – 1), or 5(4) = 20.
You could've also distributed the above equation, and solve the formed quadratic by FACTORING to get the same result: n = 5.
, as 5(5 – 1), or 5(4) = 20.
You could've also distributed the above equation, and solve the formed quadratic by FACTORING to get the same result: n = 5.