SOLUTION: A survey of 100 students asked if they studied a foreign language. The result showed: Spanish, 28; German, 30; French, 42; Spanish and German, 8; Spanish and French,10; German and

Let S be the subset of the 100 students studying Spanish, and let |S| be the cardinality of the subset S. We are given |S| = 28.

Let G be the subset of the 100 students studying German, and let |G| be the cardinality of the subset G. We are given |G| = 30.

Let F be the subset of the 100 students studying French, and let |F| be the cardinality of the subset F. We are given |F| = 42.

Let SG be the subset of the 100 students studying Spanish and German. 
    It is the intersection of the sets S and G. 
    And let |SG| be the cardinality of the subset SG. We are given |SG| = 8.

Let SF be the subset of the 100 students studying Spanish and French. 
    It is the intersection of the sets S and F. 
    And let |SF| be the cardinality of the subset SF. We are given |SF| = 10.

Let GF be the subset of the 100 students studying German and French. 
    It is the intersection of the sets G and F. 
    And let |GF| be the cardinality of the subset GF. We are given |GF| = 5.

Finally, let SGF be the subset of the 100 students studying Spanish, German and French. 
    It is the intersection of the sets S, G and F. 
    And let |SGF| be the cardinality of the subset SGF. We are given |GF| = 3.


Now, the number of students among of 100 surveyed who studies at least one of these three languages is

   N = |S| + |G| +|F| - |SG| - |SF| - |GF| + |SGF| = 28 + 30 + 42 - 8 - 10 - 5 + 3 = 80.

Thus 80 students of 100 learn at least one language.
The rest of 100, 100-80 = 20, do not study these languages.


Therefore, the probability that a randomly selected student studied no foreign language is  = .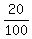


Answer.  The probability that a randomly selected student studied no foreign language is .