SOLUTION: In the context of binomial expansion, where X is the random variable, X^8=(x^5) (___) how do I find the missing factor?

Algebra ->  Statistics  -> Binomial-probability -> SOLUTION: In the context of binomial expansion, where X is the random variable, X^8=(x^5) (___) how do I find the missing factor?      Log On


   

Question 1023823: In the context of binomial expansion, where X is the random variable, X^8=(x^5) (___) how do I find the missing factor?
Answer by mathmate(429) About Me  (Show Source):
You can put this solution on YOUR website!

Question:
In the context of binomial expansion, where X is the random variable, X^8=(x^5) (___) how do I find the missing factor?

Solution:

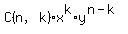When a binomial %28x%2By%29%5En is expanded, the result is n+1 terms, each of which equals C%28n%2Ck%29%2Ax%5Ek%2Ay%5E%28n-k%29 where
C(n,k) is the binomial coefficient of the kth term in an expansion to the power of n, and equals n!/(k!(n-k)!).

For example, in the expansion of 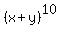%28x%2By%29%5E10, the 4th term is
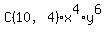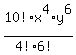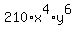
C%2810%2C4%29x%5E4%2Ay%5E6, which evaluates to 10%21%2F%284%216%21%29%2Ax%5E4%2Ay%5E6, or 210%2Ax%5E4%2Ay%5E6

The given problem probably refers to the expansion of (1+x)^8. So you can find the coefficient directly from C(8,5).