|
Question 91198: Prove that cube root of 7 is an IRRATIONAL number.
Found 3 solutions by stanbon, cparks1000000, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Prove that cube root of 7 is an IRRATIONAL number ?
Assume that cube rt 7 is rational.
Then (7)^(1/3) = a/b where a and b are integers and a/b is reduced to lowest terms.
Then a=b[7^(1/3)]
Since a is a multiple of b and a is an integer, b divides a.
Since b divides a, a = nb and n is an integer.
Therefore 7^(1/3) = a/b = nb/b, so a/b is not reduced to lowest terms.
-----------
What led to this contradiction?
The assumption that 7^(1/3) was rational.
The assumption must be wrong.
Therefore 7^(1/3) if irrational.
================
Cheers,
Stan H.
Answer by cparks1000000(5)   (Show Source): (Show Source):
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let us suppose that 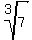 is a rational number. Then we can write is a rational number. Then we can write 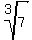 = = 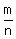 , where , where  and and  are whole numbers.
We can assume that the numbers are whole numbers.
We can assume that the numbers  and and  have no common divisor. Otherwise, we can cancel this common divisor
in the numerator and denominator.
Raise both sides of the equality have no common divisor. Otherwise, we can cancel this common divisor
in the numerator and denominator.
Raise both sides of the equality 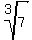 = = 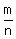 in the degree 3. You will get in the degree 3. You will get 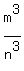 = =  . Hence, . Hence,  = = 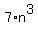 .
The right side of the last equality is divisible by .
The right side of the last equality is divisible by  . Hence, its left side . Hence, its left side  is divisible by is divisible by  also.
Since also.
Since  is divisible by is divisible by  , the whole number , the whole number  itself is divisible by itself is divisible by  .
So, we can write .
So, we can write  = = 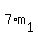 , where , where 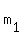 is another whole number.
Now, substitute is another whole number.
Now, substitute  = = 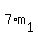 into into  = = 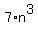 . It gives . It gives 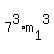 = = 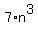 . Cancel both sides by . Cancel both sides by  . You will get . You will get 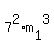 = =  .
The left side of the last equality is divisible by .
The left side of the last equality is divisible by  . Hence, its right side . Hence, its right side  is divisible by is divisible by  also.
Since also.
Since  is divisible by is divisible by  , the whole number , the whole number  itself is divisible by itself is divisible by  .
We just got a contradiction. We assumed that .
We just got a contradiction. We assumed that 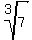 = = 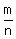 , where , where  and and  are whole numbers with no common divisor, and the chain
of arguments led us to the conclusion that both the integers are whole numbers with no common divisor, and the chain
of arguments led us to the conclusion that both the integers  and and  have the common divisor have the common divisor  .
This contradiction proves that the original assumption was wrong, regarding .
This contradiction proves that the original assumption was wrong, regarding 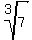 as a rational number. Hence, as a rational number. Hence, 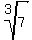 is irrational.
The proof is completed.
In the proof we used many times this property of the number 7: if 7 divides the product of two integers m and n, then 7 divides
at least one of the integers. It is the common property of any prime number in the ring of integer numbers. is irrational.
The proof is completed.
In the proof we used many times this property of the number 7: if 7 divides the product of two integers m and n, then 7 divides
at least one of the integers. It is the common property of any prime number in the ring of integer numbers.
|
|
|
| |