SOLUTION: Find all positive integers a and b so that (a+1)/b and (b+2)/a are simultaneously positive integers.

Algebra ->  Real-numbers -> SOLUTION: Find all positive integers a and b so that (a+1)/b and (b+2)/a are simultaneously positive integers.      Log On


   

Question 1138622: Find all positive integers a and b so that (a+1)/b and (b+2)/a are simultaneously
positive integers.
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


Plan of attack:

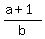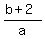Given the requirement %28a%2B1%29%2Fb equal to an integer, choose integer values for a and determine the possible integer values for b; for those possible values of b, determine whether %28b%2B2%29%2Fa is also an integer.

If a = 1...

%28a%2B1%29%2Fb+=+2%2Fb
The possible values for b are 1 and 2.
%28b%2B2%29%2Fa+=+%28b%2B2%29%2F1 is an integer for both these values of b.
For b=1, %28b%2B2%29%2Fa+=+3%2F1+=+3 --> (a,b) = (1,1) is a solution
For b=2, %28b%2B2%29%2Fa+=+4%2F1+=+4 --> (a,b) = (1,2) is a solution

If a = 2...

%28a%2B1%29%2Fb+=+3%2Fb
The possible values for b are 1 and 3.
%28b%2B2%29%2Fa+=+%28b%2B2%29%2F2 is not an integer for either b=1 or b=3.

If a = 3...

%28a%2B1%29%2Fb+=+4%2Fb
The possible values for b are 1, 2, and 4.
%28b%2B2%29%2Fa+=+%28b%2B2%29%2F3 is an integer for both b=1 and b=4.
For b=1, %28b%2B2%29%2Fa+=+3%2F3+=+1 --> (a,b) = (3,1) is a solution
For b=4, %28b%2B2%29%2Fa+=+6%2F3+=+2 --> (a,b) = (3,4) is a solution

If a = 4...

%28a%2B1%29%2Fb+=+5%2Fb
The possible values for b are 1 and 5.
%28b%2B2%29%2Fa+=+%28b%2B2%29%2F4 is not an integer for either b=1 or b=5.

If a = 5...

%28a%2B1%29%2Fb+=+6%2Fb
The possible values for b are 1, 2, 3, and 6.
%28b%2B2%29%2Fa+=+%28b%2B2%29%2F5 is an integer for b=3.
For b=3, %28b%2B2%29%2Fa+=+5%2F5+=+1 --> (a,b) = (5,3) is a solution

-----------------------------------------------------------------

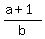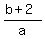I haven't been able to come up with a formal proof; but it is clear to me that there will be no solutions with values of a greater than 5. So the complete set of ordered pairs of positive integers (a,b) for which both %28a%2B1%29%2Fb and %28b%2B2%29%2Fa are both integers is
(1,1); (1,2); (3,1); (3,4); (5,3)

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
     Here's the strategy 
greenestamps was looking for:

Find all positive integers a and b so that (a+1)/b and (b+2)/a are simultaneously
positive integers.
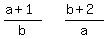matrix%281%2C4%2C%28a%2B1%29%2Fb%2C%22%22%2C%22%22%2C+%28b%2B2%29%2Fa%29%29
Those are positive integers, so
system%281%3C=%28a%2B1%29%2Fb%2C+1%3C=%28b%2B2%29%2Fa%29
system%28b%3C=a%2B1%2C+a%3C=b%2B2%29
Add 1 to both sides of the second inequality
system%28b%3C=a%2B1%2C+a%2B1%3C=b%2B3%29
Those inequalities can be combined as
b%3C=a%2B1%3C=b%2B3
So we have four cases: a+1=b, a+1=b+1, a+1=b+2, a+1=b+3
which simplify to a=b-1, a=b, a=b+1, a=b+2

Case 1:  a=b-1 substitute in 


For the expression to be a positive integer,
b-1 is either 1 or 3.
For b-1=1 or b=2 and a=b-1=2-1=1, (a,b)=(1,2)
For b-1=3 or b=4 and a=b-1=4-1=3, (a,b)=(3,4)

Case 2:  a=b substitute in 

Those will both be integers only if b=1. 
a=b=1, (a,b)=(1,1) 

Case 3:  a=b+1 substitute in 


For the second expression to be a positive integer,
b+1 must be 1, which makes b=0. So we must discard 
Case 3 as impossible. 

Case 4:  a=b+2 substitute in 

For the first expression to be a positive integer,
b is either 1 or 3.
For b=1, a=b+2=1+2=3, so (a,b)=(3,1) is a solution.
For b=3, a=b+2=3+2=5, so (a,b)=(5,3) is a solution.

So there are 5 solutions:
(a,b)=(1,2)
(a,b)=(3,4) 
(a,b)=(1,1)
(a,b)=(3,1)
(a,b)=(5,3)

Edwin