|
Tutors Answer Your Questions about real-numbers (FREE)
Question 1209262: True or false
(a) If p is rational, then p^2 is rational.
(b) If p is irrational, then p^2 is irrational.
(c) If p^2 is rational, then p is rational
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1208451: The safe load, L, of a wooden beam supported at both ends varies jointly as the width, w, and the square of the depth, d, and inversely as the length, l. A wooden beam 8in.
wide, 8in.
deep, and 5ft
long holds up 15106lb
. What load would a beam 9in.
wide, 5in.
deep, and 18ft
. long, of the same material, support? Round your answer to the nearest integer if necessary..
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If you are going to find the safe loads for several different sets of parameter values, then do as the other tutor says and use the given information to determine the proportionality constant k, and then use the formula and that value of k to find the safe loads for the other sets of parameter values.
If you only need to find the answer to this single problem, there is no need to determine the proportionality constant.
For the given set of parameter values, the safe load is 15106 pounds.
The safe load varies directly as the width of the beam. From the given set of parameters to the new set, the width changes by a factor of 9/8, so that change in the width changes the safe load by a factor of 9/8.
The safe load varies directly as the square of the depth of the beam. From the given set of data to the new set, the depth changes by a factor of 5/8, so that change in depth changes the safe load by a factor of (5/8)^2 = 25/64.
The safe load varies inversely as the length of the beam. From the given set of data to the new set, the length changes by a factor of 18/5, so that change in length changes the safe load by a factor of 5/18.
So the combination of changes in the parameters changes the safe load by a factor of
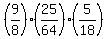
So the safe load with the new set of parameters is
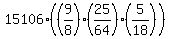
Use a calculator to find the safe load with the new set of parameters is, to the nearest pound, 1844 pounds.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1208452:
Answer by timofer(104)  (Show Source): (Show Source):
Question 1208400: List the numbers in set F that are natural, integers, rational, irrational and real.
F = {-sqrt{2}, pi + sqrt{2}, (1/2) + 10.3}
Natural = none
Integers = none
Rational = (1/2) + 10.3
Irrational = every element in set F
Real = every element in set F
You say?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In your post, you say "Irrational = every element in set F".
It is not correct. Element (1/2) + 10.3 of F is a rational number.
So, it should be fixed.
The other answers are correct.
Question 1208268: is -5 irrational?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Integer numbers live in heaven (like in paradise).
They enjoy all the pleasures of living in paradise. (Like American retired people after 40 years hardworking).
Rational numbers live in purgatory. (Like American retired people after 10-15 years hardworking).
Irrational numbers live in hell.
Every day and every night the devils fry them in a frying pane, extract square roots from them, and turn them inside out
by raising them in degree (-1), so they continue struggling permanently, still remaining irrational numbers forever.
Let' start raising money to beg for irrational numbers from hell.
It takes 1 (just one) cent for each irrational number.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: No, it's not irrational
Reason: We can write -5 as -5/1
Since we have a fraction or ratio of two integers, it proves that -5 is rational.
An irrational number is something like pi = 3.14... that cannot be written as a fraction of two integers.
Question 1207827: A. Give an example in which the result of raising a rational number to a rational power is an irrational number.
B. Give an example in which the result of raising an irrational number to a rational power is a rational number.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1207826: Give an example of irrational numbers a and b such that the indicated expression is (a)rational and (b)irrational.
A. a + b
B. a - b
C. a•b
D. a/b
I would 2 samples for each, if possible.
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1207368: Can an irrational number raised to an irrational power yield an answer that is rational? This problem shows that the answer is “yes.” (However, if you study the following solution very carefully, you’ll see that even though we’ve answered the question in the affirmative, we’ve not pinpointed the specific case in which an irrational number raised to an irrational power is rational.)
(a) Let A = (sqrt{2})^(sqrt{2}). Now, either A is rational or A is irrational. If A is rational, we are done. Why?
(b) If A is irrational, we are done. Why?
Hint:Consider A^(sqrt{2}).
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a soup of words with zero mathematical meaning.
Did I say " . . . with zero mathematical meaning" ?
No. it is not right. It is better to say " with negative mathematical meaning ".
So, it is better to glue up your eyes and ears with adhesive tape
so as not to see or hear this MEGA-gibberish.
Question 1206550: per-pupil costs (in thousands of dollars) for cyber charter school tuition for school districts in three areas are shown. test the claim that there is a difference in means for the three areas, using an appropriate parametric test. area 1 6.2 9.3 6.8 b.1 b.7 7.5 area 2 7.5 8.2 8.5 8.2 7.0 9.3 area 3 5.8 6.4 5.6 7.1 3.0 3.0 solution: ss de
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
per-pupil costs (in thousands of dollars) for cyber charter school tuition for school districts
in three areas are shown. test the claim that there is a difference in means for the three areas, using an appropriate parametric test.
area 1 6.2 9.3 6.8 b.1 b.7 7.5
area 2 7.5 8.2 8.5 8.2 7.0 9.3
area 3 5.8 6.4 5.6 7.1 3.0 3.0
solution: ss de
~~~~~~~~~~~~~~~~~~~~~~
What does the letter "b" mean inside the numerical data, printed in the post ?
Is it a mistake ? result of negligence ?
Question 1206522: State with a cogent reason whether or not the relationship: y=√x³ represents y as a function of x for both variables coming from the real number system
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem does not use good mathematical language....
My guess as to the meaning of "... for both variables coming from the real number system" is that the set of all real numbers is both the domain and range of the function.
In that case, the relation  does not satisfy that condition, because y is not real when x is negative. does not satisfy that condition, because y is not real when x is negative.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1206491: is -36/4 an integer or non integer
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1206313: The set of all y such that y - 2 is greater than -5 and less than or equal to 7.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
They want you solve this compound inequality
-5 < y-2 <= 7.
Add 2 to the left, middle and right sides of this inequality. You will get
-5+2 < (y-2) + 2 <= 7+2,
or
-3 < y <= 9.
At this point, the problem is just solved.
The solution is this infinite set of real numbers -3 < y <= 9. ANSWER
Solved.
---------------
On solving compound inequalities, see the lesson
- Solving compound inequalities
in this site.
Find there many other similar and different problems with detailed solutions and complete explanations.
Learn the subject from there ( ! )
Question 1206291: The set of all y such that y - 2 is greater than -5 and less than or equal to 7.
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
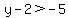 and and 
or, put it this way



The set of all  is: { is: {  , , , , , , , , , , , , , , , , , , , , , ,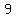 } }

Question 1206149: I need help with the last two problems.

Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Although you only asked for the last two problems, I'll go over all four problems. It could be helpful for any future student.
Problem 1
Domain: (-∞, ∞)
This represents the set of all real numbers. This is because we can plug in any real number for x and the output is always 5.
(-∞, ∞) represents -∞ < x < ∞
Infinity is not a number but we can think of it informally as such.
--------------------------------------------------------------------------
Problem 2
Domain: (-∞, ∞)
We have the same idea as the previous problem. Except this time the output isn't always 5.
--------------------------------------------------------------------------
Problem 3
Domain: (-∞, -1/2) U (-1/2, ∞)
Recall we cannot divide by zero.
If the denominator -2x-1 was zero, then,
-2x-1 = 0
-2x = 1
x = -1/2
Follow the chain backwards to find that x = -1/2 makes the denominator zero.
Therefore we must kick x = -1/2 out of the domain. Any other real number is a valid input.
The real number line (-∞, ∞) will have a hole poked in it at -1/2 to end up with (-∞, -1/2) U (-1/2, ∞)
(-∞, -1/2) represents x < -1/2 aka -∞ < x < -1/2
(-1/2, ∞) represents x > -1/2 aka -1/2 < x < ∞
The union symbol "U" represents "or".
--------------------------------------------------------------------------
Problem 4
Domain: (-∞, -3) U (-1, ∞)
We cannot have 0 in the denominator. Furthermore, we cannot have the stuff under the square root be negative.
x^2+4x+3 must be positive.
Use any of the following techniques to solve x^2+4x+3 = 0- Graphing (look at the x intercepts)
- Completing the square
- Quadratic formula
- Factoring
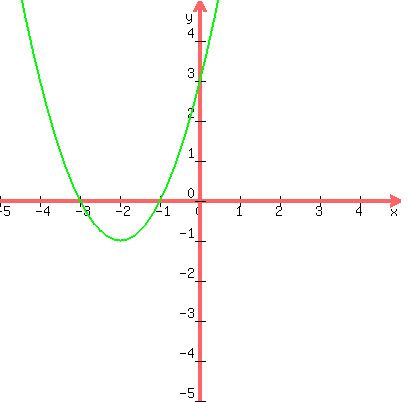
Whichever method you use, you should find the x intercepts are -3 and -1.
The parabola on the interval -3 < x < -1 dips below the x axis.
The portions x < -3 and x > -1 are above the x axis.
So that explains the portions (-∞, -3) and (-1, ∞)
(-∞, -3) represents x < -3 aka -∞ < x < -3
(-1, ∞) represents x > -1 aka -1 < x < ∞
Graph of y = x^2+4x+3
Question 1206067: Evaluate the piecewise defined function at the indicated values.
f(x) = 2 if x ≤ 4
= 4x − 3 if x > 4
f(−5) =
f(0) =
f(4) =
f(5) =
f(7) =
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To evaluate a piecewise function, you always do/perform the same procedure.
First, for given value of argument x, you identify to which interval x does belong.
It says to you, which formula to use.
As soon as you identified which formula to use - - - use it.
For example, for (a), the argument -5 does belong to x <= 4;
so, you use the first line formula,
and it gives you f(-5) = 2. ANSWER
Next case, for (b), the argument 0 does belong to x <= 4;
so, you use the first line formula,
and it gives you f(0) = 2. ANSWER
Next case, for (c), the argument 4 does belong to x <= 4;
so, you use the first line formula,
and it gives you f(4) = 2. ANSWER
Next case, for (d), the argument 5 does belong to x > 4;
so, you use the second line formula,
and it gives you f(5) = 4*5 − 3 = 17. ANSWER
Make the last case on your own, guided by my instructions.
Happy calculations (!)
The major lesson to learn from my post is that this job is EASY to do.
Question 1204881: Tell which real number corresponds to the situation.
During a year, a person saves 1500 dollars.
What is the corresponding number for this sentence?
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1204219: I need to factor h^3-25. I've tried but I always get h in there. I've done (h)(h+5)(h-5) or (h)(h^2-25) but I always get h^3-25h. There is no perfect cube so I am struggling. Thank you
Found 4 solutions by math_tutor2020, Alan3354, MathLover1, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
It's possible that the original expression is h^3 - 125
If so, then use the difference of cubes factoring rule
a^3 - b^3 = (a-b)(a^2 + ab + b^2)
to find that,
h^3 - 125 = (h-5)(h^2 + 5h + 25)
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! I need to factor h^3-25. I've tried but I always get h in there. I've done (h)(h+5)(h-5) or (h)(h^2-25) but I always get h^3-25h. There is no perfect cube so I am struggling. Thank you
=================
Maybe it's h^3 - 125?
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I need to factor h^3-25. I've tried but I always get h in there. I've done (h)(h+5)(h-5) or (h)(h^2-25)
but I always get h^3-25h. There is no perfect cube so I am struggling. Thank you
~~~~~~~~~~~~~~~~
To factor " h^3 - 25 " is WRONG assignment.
It is NOT POSSIBLE to factor it with integer degrees and integer coefficients.
Even do not try.
Do not spend your time for nothing.
What is the source of your assignment ?
This source is FALSE, equally as this assignment itself.
Do not forget to post your THANKS to me for saving you from doing this non-sensical job.
Question 1204033: what set does -7 belong to
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1203869: find the range of f(x) = sqrt(floor(x)-3)
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1203870: find the range of f(x) = sqrt(floor(x)-3)
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1203734: What set does 5 1/3 and 3 belong to?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
They do belong to many different sets.
For example, they both belong to the set of all rational numbers.
As another example, they both belong to the set of all positive rational numbers.
They both belong to the set of all real numbers.
They both belong to the set of all positive real numbers.
Etc.
Question 1203099: If we place a 3 at both ends of a number, its value is increased by 3372. Find the original number.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If we place a 3 at both ends of an  number, its value is increased by 3372. number, its value is increased by 3372.
Find the original number.
~~~~~~~~~~~~~~~~~~
Let the original integer number be x.
It is almost obvious (and easy to show) that the original number is a two-digit number.
If we place a 3 at both ends of such a number, its value becomes 3000+10x+3.
Therefore, according to the condition, we should find x from this equation
(3000 + 10x + 3) - x = 3372.
It is easy
10x - x = 3372 - 3000 - 3
9x = 369
x = 369/9 = 41.
CHECK. 3413 - 41 = 3372, the increase value. ! correct !
ANSWER. The original number is 41.
Solved.
Question 1203095: When Ibuprofen is given for fever to children 6 months of age up to 2 years, the usual dose is 5 milligrams (mg) per kilogram (kg) of body weight when the fever is under 102.5 degrees Fahrenheit. How much medicine would be usual dose for a 18 month old weighing 45.3 pounds?
______ milligrams
Found 2 solutions by MathLover1, josgarithmetic:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! -------------------------------
..., weighing 45.3 pounds?
-------------------------------
Identify the needed ratio in the description.
5 milligrams Ibuprofen per 1 kilogram body weight.
KNOW or find the needed unit conversion ratio of 453.59 grams per 1 pound.
Do the rest!
Question 1203072: Four 3-megawatt wind turbines can supply enough electricity to power 3000 homes.
How many turbines would be required to power 25898 homes? __________ 3 megawatt turbines. Round to the nearest whole number.
Found 3 solutions by greenestamps, math_tutor2020, josgarithmetic:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other two responses are rather formal -- which is fine, but perhaps not necessary.
There is presumably a direct relationship between the number of turbines and the number of homes. So simply multiply the given 4 turbines by the ratio of the numbers of turbines:
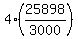 = 34.53 to 2 decimal places. = 34.53 to 2 decimal places.
ANSWER: to the nearest whole number, 35 turbines
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
4 turbines power 3000 homes.
This would mean 1 turbine powers 3000/4 = 750 homes.
n = number of turbines
750n = number of homes powered by n turbines
750n = 25898
n = 25898/750
n = 34.5306666666667 approximately
Round this up to the nearest whole number so we clear the hurdle.
Having 34 turbines will come up short of the goal of powering 25898 homes (since 34 turbines would power 34*750 = 25500 homes)
Therefore, 35 turbines are needed.
--------------------
Another approach
(numberOfTurbines)/(numberOfHomes) = (numberOfTurbines)/(numberOfHomes)
n/25898 = 4/3000
3000n = 25898*4
n = 25898*4/3000
n = 34.5306666666667 approximately
n = 35 when rounding up to the nearest integer
--------------------
Answer: 35
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1203089: x*y=2x-y find the value of y if y*(3*y)=6
Found 4 solutions by ikleyn, math_tutor2020, Theo, Alan3354:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
In many other contexts, the asterisk or star symbol * indicates multiplication.
Example: 2*3 = 6
However, this problem has the star operator redefined as:
x*y = 2x-y
This is a user-defined operator.
It is not to be confused with the multiplication symbol.
So be careful not to assume that y*(3*y) turns into 3y^2
Let's replace x with 3
x*y = 2x-y
3*y = 2(3)-y
3*y = 6-y
This means any time we see 3*y, we can replace it with 6-y.
x*y = 2x-y
x*(3*y) = 2x-(3*y)
x*(3*y) = 2x-(6-y)
x*(3*y) = 2x-6+y
x*(3*y) = 2x+y-6
Next we'll replace x with y so we end up with y*(3*y)
x*(3*y) = 2x+y-6
y*(3*y) = 2y+y-6
y*(3*y) = 3y-6
We're told that y*(3*y) = 6
We'll use the previous equation and this given fact to solve for y.
y*(3*y) = 6
3y-6 = 6
3y = 6+6
3y = 12
y = 12/3
y = 4
Answer: y = 4
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your two equations are:
x*y=2x-y
y*(3*y)=6
simplify to get:
x*y = 2x - y
3y^2 = 6
in the first equation:
add y to both sides of the equation to get x*y + y = 2x
factor out the y to get:
y * (x + 1) = 2x
solve for y to get:
y = 2x / (x + 1)
in the second equation solve for y^2 to get:
y^2 = 2
since y = 2x / (x + 1), then:
y^2 = 4x^2 / (x^2 + 2x + 1)
your equation of y^2 = 2 becomes:
4x^2 / (x^2 + 2x + 1) = 2
multiply both sides of this equation by (x^2 + 2x + 1) to get:
4x^2 = 2 * (x^2 + 2x + 1)
simplify to ge:
4x^2 = 2x^2 + 4x + 2
subtract the right hand side of the equation from both sides of the equation to get:
4x^2 - 2x^2 - 4x - 2 = 0
combine like terms to get:
2x^2 - 4x - 2 = 0
factor out a 2 to get:
x^2 - 2x - 1 = 0
factor this quadratic equation to get:
x = 2.4142135623731 or x = -0.4142135623731
to confirm, replace x with either of these values in the original equation to solve the original problem.
the original problem gives you the original equation of x*y=2x-y.
it then asks you to find the value of y if y * (3 * y) = 6
i think it might be asking you to find the value of x is y * (3 * y) = 6
i solved for x to get the values of x above.
i also solved for y in the second equation to get y^2 = 2
thqat would make y equal to plus or minus sqrt(2).
using the values of x above, i replaced x in the original equation of x*y = (2x -y,
solving for y in that equation, i got y = 2x / (x + 1).
using the value of x i derived above, i got y = plus or minus sqrt(2).
i graphed both equation and got what you see below:

your solution is that y = sqrt(2) when x = 2.4142135623731 and y = -sqrt(2) when x = -0.4142135623731.
alternatively, your solution is that x = 2.4142135623731 when y = sqrt(2) and x = -0.4142135623731 when y = -sqrt(2).
i used a quadratic solver to find the values of x.
here are the results from that quadratic equation solver.

not that y = -1.414 and y 1.414 that you see on the graph is a rounded version of y = -sqrt(2) and y = sqrt(2).
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1202869: Please help me solve these equations
1) x + y + z = 3
x + 2y - z = 2
x + yz + zx = 3
2) x +yz = 2
y + zx = 2
z + xy = 2
Found 3 solutions by MathTherapy, ikleyn, Alan3354:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x + 2y - z = 2
x + yz + zx = 3
2) x +yz = 2
y + zx = 2
z + xy = 2
I'll do # 1 for you. Apply the same concept and you should have no problems doing # 2.
x + y + z = 3______x + y = 3 - z --- eq (i)
x + 2y - z = 2 ------- eq (ii)
x + yz + xz = 3 ------- eq (iii)
2x + 2y + 2z = 6 ----- Multiplying eq (i) by 2 ------ eq (iv)
x + 2y - z = 2 ----- eq (ii)
x + 3z = 4 ----- Subtracting eq (ii) from (iv)
x = 4 - 3z ----- eq (v)
x + yz + xz = 3____x + (y + x)z = 3 --- eq (iii)
x + (3 - z)z = 3 --- Substituting 3 - z for x + y in eq (iii)
 --- eq (vi) --- eq (vi)
 ----- Substituting 4 - 3z for x in eq (vi) ----- Substituting 4 - 3z for x in eq (vi)
 z = 1
x = 4 - 3z ------ Substituting 1 for z in eq (v)
x = 4 - 3(1)
x = 4
x = 1
x + y = 3 - z
1 + y = 3 - 1 ------- Substituting 1 for x, and 1 for z in eq (i)
y = 2
y = 1
(x, y, z) = (1, 1, 1)
z = - 1
x = 4 - 3z ------ eq (v)
x = 4 - 3(- 1) -- Substituting - 1 for z in eq (v)
x = 4 + 3
x = 7
x + y = 3 - z
7 + y = 3 - - 1 ----- Substituting 7 for x, and - 1 for z in eq (i)
7 + y = 4
y = 4 - 7
y = - 3
(x, y, z) = (7, - 3, - 1)
The fact that x, y, and z are purported to have DIFFERENT values would suggest to me that
(x, y, z) = (1, 1, 1) is NOT the solution set, but (x, y, z) = (7, - 3, - 1) instead,
would be the CORRECT solution set!!
I don't think it has to be stated that x, y, and z are different numbers. The fact that they're
given DIIFERENT variables would automatically mean that they are.
I believe, wholeheartedly, that a note should've been attached to this problem, stating that
z = 1
x = 4 - 3z ------ Substituting 1 for z in eq (v)
x = 4 - 3(1)
x = 4
x = 1
x + y = 3 - z
1 + y = 3 - 1 ------- Substituting 1 for x, and 1 for z in eq (i)
y = 2
y = 1
(x, y, z) = (1, 1, 1)
z = - 1
x = 4 - 3z ------ eq (v)
x = 4 - 3(- 1) -- Substituting - 1 for z in eq (v)
x = 4 + 3
x = 7
x + y = 3 - z
7 + y = 3 - - 1 ----- Substituting 7 for x, and - 1 for z in eq (i)
7 + y = 4
y = 4 - 7
y = - 3
(x, y, z) = (7, - 3, - 1)
The fact that x, y, and z are purported to have DIFFERENT values would suggest to me that
(x, y, z) = (1, 1, 1) is NOT the solution set, but (x, y, z) = (7, - 3, - 1) instead,
would be the CORRECT solution set!!
I don't think it has to be stated that x, y, and z are different numbers. The fact that they're
given DIIFERENT variables would automatically mean that they are.
I believe, wholeheartedly, that a note should've been attached to this problem, stating that 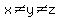 . .
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the system of equations
x + yz = 2, (1)
y + zx = 2, (2)
z + xy = 2. (3)
~~~~~~~~~~~~~~~~~~~~~~~~
ANSWER. There are two sets of solutions: (a) (x,y,z) = (1,1,1) and (b) (x,y,z) = (-2,-2,-2).
Solution
First, it is easy to see by inspection that x = y = z = 1 is the solution.
Next, our goal is to check if there are other solutions.
Let's assume x= 1. Then equations (1) and (2) take the forms
1 + yz = 2, (1')
y + z = 2. (2')
From (2'), express z = 2-y and substitute it into equation (1'). You will get
1 + y*(2-y) = 2 --> 1 + 2y - y^2 = 2 --> y^2 - 2y + 1 = 0 --> (y-1)^2 = 0 --> y= 1. (4)
Thus if we assume x= 1, then y= 1 and similarly z= 1.
In the same way, if we assume that any single variable is 1, then we get
that two other variables are equal to 1, due to equations.
So, if we are looking for other sets of solutions,
where at least one unknown is not equal to 1,
then no one of the three unknowns in these sets is 1.
+-----------------------------------------------------+
| OK, this step of reasoning is complete. |
| At this point, we start next step of reasoning. |
+-----------------------------------------------------+
From equations (1) and (2)
x + yz = y + zx,
(x-y) - (xz - yz) = 0,
(x-y) - z(x-y) = 0,
(1-z)*(x-y) = 0.
Since we assume now that z =/= 1, we come to x = y. (5)
Similarly, from equations (1) and (3) we come to x = z. (6)
Similarly, from equations (2) and (3) we come to y = z. (7)
+--------------------------------------------------+
| Let before the last attack w denotes |
| any of the three equal quantities x = y = z. |
+--------------------------------------------------+
Then equation (1) takes the form
w + w^2 = 2 --> w^2 + w - 2 = 0 --> factoring (w-1)*(w+2) = 0 --> w = 1 or w = -2.
Thus we get these triples (x,y,z) = (1,1,1) and (x,y,z) = (-2,-2,-2), that we announced as the solutions at the beginning.
Easy check confirms that (x,y,z) = (-2,-2,-2) is the second solution set.
There is NO any other solutions.
Solved.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me solve these equations
1) x + y + z = 3
x + 2y - z = 2
x + yz + zx = 3
2) x +yz = 2
y + zx = 2
z + xy = 2
------------------------
x = y = z = 1 for both, by inspection
Question 1202601: set p consists of all the prime numbers among the first 100 positive integers. set e consists of all the even numbers among the first 100 positive integers. which of the following must be true?
1. Set P contains more numbers than Set E.
2, The intersection of the two sets contains exactly one number.
3. The union of the two sets contains exactly one number.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:- False
- True
- False
------------------------------------------------------------------------------------
Explanation for Problem 1)
There are 100 values in the set {1,2,3,...,98,99,100}
Cut that in half to find there are 100/2 = 50 even numbers {2,4,6,...,96,98,100}
There are 50 elements in set E.
The other 50 elements are odd numbers {1,3,5,...,95,97,99} some of those are prime.
1 is not prime
3 is prime
5 is prime
7 is prime
9 is not prime
11 is prime
13 is prime
15 is not prime
17 is prime
19 is prime
21 is not prime
etc
Since we're kicking out values that aren't prime, we go from 50 elements to something smaller. Even when considering the even prime 2, the set of primes between 1 and 100 will not exceed 50 values.
This is enough to prove that set P has fewer items than set E.
Statement 1 is proven false.
----------------
Explanation for Problem 2)
This statement is true because the intersections of these two sets - E = {2,4,6,...,96,98,100}
- P = primes between 1 and 100
consists of the singleton set {2}
Nearly everything in set P is odd. The single exception is the value 2.
The value 2 is both prime and an even number. It is the only even number prime.
Every other even number is composite because 2 is a factor.
----------------
Explanation for Problem 3)
Consider this example
A = {1,2,3}
B = {3,7,8,9}
Then
A union B = {1,2,3,7,8,9}
We combine the two sets into one big set. Toss any duplicates.
Now we must find the union of:
E = {2,4,6,...,96,98,100}
P = set of primes between 1 and 100
It should be fairly clear that we cannot obtain a set of 1 item when unioning sets E and P
The number of items in set E u P will be at least 50 values. That 50 referring to the number of items in set E.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write to us what do  think about it. think about it.
We will check and respond to you (on the free of charge basis).
It does not require deep knowledge.
The smallest spark of thought in your head is just enough.
Question 930689: Find the smallest natural number that is simultaneously the sum of 9, 10 and 11
consecutive integers.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor has nothing to do with the given problem....
Let the three strings of consecutive integers be
a(1), ..., a(9)
b(1), ..., b(10)
c(1), ..., c(11)
The sum of the each sequence is the number of terms in the sequence, multiplied by the average of the first and last terms.
First sequence...
The average of 9 consecutive integers is an integer;
The sum is 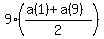
Second sequence...
The average of 10 consecutive integers is not an integer, but the sum of the first and last integers is an integer;
The sum is  = = 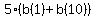
Third sequence...
The average of 11 consecutive integers is an integer;
The sum is 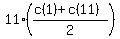
The three sums are to be the same; that means the sum must be a multiple of 9, 5, and 11. The least common multiple of 9, 5, and 11 is 495; and that is the answer to the problem.
First sequence: 495 = 9(55) = 51+52+...+58+59
Second sequence: 495 = 10(49.5) = 5(99) = 45+46+...+53+54
Third sequence: 495 = 11(45) = 40+41+...+49+50
ANSWER: 495
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590
|
| |






