Question 719537: solve log(127/27) in terms of log2,log3 and log5 to any base.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! These problems where you're asked to express one logarithm in terms of a certain set of given logs usually involves finding a way to express the log in terms of logs of products, quotients or powers of the arguments of the given logs. In this problem we will try to express log(127/27) in terms of logs (of any base) of products, quotients and/or powers of 2's, 3's and/or 5's.
What is often overlooked in these types of problems is: logs of powers of the base of that log. For example, if we were trying to express something in terms of base 10 logs of 2, 3 or 5, we can also use logs of powers of 10. We can do this because base 10 logs of powers of 10 simplify to a simple number.
When looking at log(127/27) we might see that the 27 could be expressed as a power of 3:  . But what about the 127? 127 is prime. It is not a product, quotient and/or power of 2's, 3's and/or 5's. The only way we can handle the 127 is: To use base 127 logs!
So we will start by using the base conversion formula,  to convert the log(127/27) to base 127 logs:
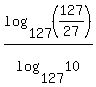
Now we can use a property of logarithms,  , to rewrite the log in the numerator:
The first log is the base 127 log of a known power of 127, i.e.  . So that log is a 1:
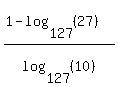
For the remaining logs we can express the numerator's argument as a power of 3 and the denominator's argument as a product of 2 and 5:
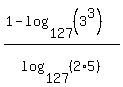
For the log in the numerator we can use another property of logarithms,  . For the log in the denominator we can use a third property logs:  .
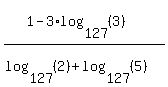
We have now expressed
in terms of base 127 logs of 2's, 3's and 5's:
|
|
|
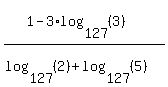
