SOLUTION: how to solve -2*e^(-3n-8)-3=-45

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: how to solve -2*e^(-3n-8)-3=-45      Log On


   

Question 594712: how to solve -2*e^(-3n-8)-3=-45
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
-2%2Ae%5E%28-3n-8%29-3+=+-45
For an equation where the variable is in an exponent, like this one, start by isolating the base and its exponent. So we'll start by adding 3:
-2%2Ae%5E%28-3n-8%29+=+-42
and then dividing by -2:
e%5E%28-3n-8%29+=+21

The next step is to find the logarithm of each side. A logarithm of any base may be used. But there are advantages to choosing certain bases:
  • Matching the base of the logarithm to the base of the exponent will result in a simpler expression.
  • Choosing base 10 (aka "common") logarithm or a base e (aka natural logarithm (ln)) will result in an expression that can be evaluated with a calculator (if a decimal answer is required or needed).

For your equation choosing base e (ln) will give us both advantages: a simpler expression that can also be evaluated with a calculator. (I'll do it with logs of other bases at the end so you can see what happens.)

Finding the ln of each side we get:
ln%28e%5E%28-3n-8%29%29+=+ln%2821%29
Now we use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponent of the argument out in front of the log. It is this property that is the very reason we use logarithms. This property allows us to move the exponent, where the variable is, "down to earth". Once the variable out of the exponent we can use regular algebra to solve for it. Using this property on our equation we get:
%28-3n-8%29%2Aln%28e%29+=+ln%2821%29

First we simplify. By definition ln(e) = 1 (this is why matching the base of the log and the base of the exponent results in simpler expressions) so the equation is now:
-3n-8+=+ln%2821%29
Now we just add 8:
-3n+=+ln%2821%29+%2B+8
and divide by -3:
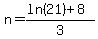
n+=+%28ln%2821%29+%2B+8%29%2F3
This is an exact expression for the answer. If you want or need a decimal approximation, get out your calculator.

Let's see what happens if you use a different base of logarithm on
e%5E%28-3n-8%29+=+21
Let's try base 10:
log%28%28e%5E%28-3n-8%29%29%29+=+log%28%2821%29%29
%28-3n-8%29%2Alog%28%28e%29%29+=+log%28%2821%29%29
This time, log(e) is not a 1 so it doesn't "disappear". Dividing by log(e) we get:
-3n-8+=+log%28%2821%29%29%2Flog%28%28e%29%29
-3n+=+log%28%2821%29%29%2Flog%28%28e%29%29+%2B+8
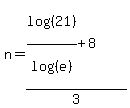
n+=+%28log%28%2821%29%29%2Flog%28%28e%29%29+%2B+8%29%2F3

n+=+%28log%28%2821%29%29+%2B+8%2Alog%28%28e%29%29%29%2F%283%2Alog%28%28e%29%29%29
This is another exact expression for the answer. It's not as simple but still correct. (If you don't believe me, get out your calculator and compare the decimals for this and for the answer we got earlier. (Note: Because these are decimal approximations, there may be a very small difference in the two decimals.)

One more time with another base. Let's try base 7 logs. (There is no good reason to choose base 7 but I'm doing this to illustrate that any base can be used.)
e%5E%28-3n-8%29+=+21
log%287%2C+%28e%5E%28-3n-8%29%29%29+=+log%287%2C+%2821%29%29
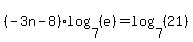
%28-3n-8%29%2Alog%287%2C+%28e%29%29+=+log%287%2C+%2821%29%29
This time, log(e) is not a 1 so it doesn't "disappear". Dividing by 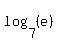log%287%2C+%28e%29%29 we get:
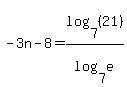
-3n-8+=+log%287%2C+%2821%29%29%2Flog%287%2C+e%29%29
-3n+=+log%287%2C+%2821%29%29%2Flog%287%2C+%28e%29%29+%2B+8
n+=+%28log%287%2C+%2821%29%29%2Flog%287%2C+%28e%29%29+%2B+8%29%2F3


This is yet another exact expression for the answer. It is just as complex as the base 10 answer but you cannot use a calculator to find base 7 logs!? (To get a decimal approximation from this expression, you would have to use the change of base formula to change all those base 7 logs into base 10 or base e logs. If you went through with all that you'd find that the decimal you get will be the same as the ones from the earlier solutions.