Question 251354: Use the formula N = Iekt, where N is the number of items in terms of the initial population I, at time t, and k is the growth constant equal to the percent of growth per unit of time. There are currently 63 million cars in a certain country, decreasing by 6.9% annually. How many years will it take for this country to have 33 million cars? Round to the nearest year.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I'm not sure I understand the description of "I". If "I" stands for the initial number of cars (i.e. the number of cars at t = 0), then the following solution will work.
Rarely does one use a percent as a percent in any arithmetic. You just about always will use the decimal or fraction equivalent of the percent. Since a decrease of 6.9% is equivalent to -0.069, the problem is to find t when N = 33 and I = 63 and k = -0.069:
To solve an equation with the variable in an exponent like this, logarithms are usually used. But first we'll isolate the exponentiated factor by dividing both sides by 63:
Now we will use logarithms. Any base can be used. But since we want a decimal approximation of the answer, we should choose a base that our calculator can find. If your calculator can do natural logarithms, "ln", this would be best because the base of natural logarithms is e and we have e in the equation. (I will also solve this using base 10 logarithms in case this is the only base your calculator can do.)
Finding the natural log of each side we get:
Next we use a property of logarithms,  , to move the exponent of the argument out in front. (Being able to use this property to move the exponent like this is the reason we use logarithms to solve these problems with variables in the exponent. Somehow we have to get the variable out of the exponent and this property is the most common way to do this.)
Since ln(e) = 1 by definition this becomes:
Next we can divide both sides by -0.069:
This is an exact answer for t.
Before we get to a decimal approximation for it, I'd like to show you how base 10 logarithms would work on this problem. With base 10 logarithms the steps would be the same up to a certain point. Instead of
we would get
From here it is a little different due to the fact that  is not 1. So we proceed by dividing both sides by  :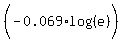
This is another exact expression for t.
Both exact expressions, though they look different, are correct. Either one can be used to find a decimal approximation. We will need a calculator (or calculator software on a computer) that can do either base 10 or natural logarithms. If your calculator can work with expressions with parentheses, then you can just pretty much type in what you see. If not, here's some steps you can use:- Find 33/63
- Find the logarithm of the 33/63
- Divide this logarithm by -0.069. (If you are using natural logarithms then you are finished. If you are using base 10 logarithms, continue.)
- A decimal approximation for e is 2.7182818284590451. Use this (or a rounded off version of this) and find its base 10 logarithm.
- Divide the result from step #3 by the result from step #4.
With either logarithm we should get something close to 9.3714081873196008. Rounding to the nearest year we find that the number of cars will become 33 million in about 9 years.
|
|
|
