Question 124442: Use the change of base formula to solve log10 (e)
A 0.891
B 1.458
C 0.434
D 1.653
E 0.422
F 0.123
I tried what I thought was the correct way of solving this,but i came to an answer which isnt a choice,so im not sure what to try.
If someone could show me the steps to come to the correct answer it would be very much appriciated. Thank you very much for your time!
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Just for grins, let's find the answer using a calculator. First let's find the value of e
by entering 1 on the calculator, then pressing the  key. You should see the answer
2.718281828 appear. This tells you that 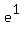 which is just e is equal to 2.718281828.
.
Then to find the log to the base 10 of that value, just press the "log" key. The answer that
should appear is 0.434294481 which rounds to 0.434. Now we know the answer to the problem.
.
Now let's see if we can get that answer by using the change of base formula.
.
The change of base formula is:
.
.
You are asked to use that formula to find:
.
.
By comparing the given problem to the left side of the change of base formula you can
see that a = 10 and x = e. Here comes the "thinking part." The natural log of e is 1. This means:
.
.
So let's say that b = e. Once we say that, we can substitute a = 10, x = e, and b = e into the
change of base formula. Start with:
.
.
Make the substitutions and you have:
.
.
but as we already know, . So we can substitute 1 for that and the change
of base formula you get:
.
.
Use your calculator to calculate 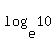 . On your calculator, enter 10 and press the "ln"
key to find that it equals 2.302585093. Substitute that value for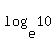
.
.
Do the division on the right side and you get:
.
.
and this rounds off to:
.
.
Unfortunately, this doesn't show why the change of base formula is really useful. As
long as you are working in the common bases 10 and e, you can pretty much do the math on a
calculator because those functions are on a calculator or can be evaluated from tables commonly
found in math books.
.
Where the change of base formula becomes really important is when you have to work with
logarithms in bases other that 10 or e. To find logarithms in unusual bases, you use the
change of base formula to convert from logs in common bases (10 and e) to get logs in
other bases. It's a powerful tool.
.
For example, suppose you need to find  . You don't find that in any common math
book or on a common scientific calculator. You can find  . So start with
the change of base formula.
.
.
If you substitute 6 for a and 50 for x this formula becomes:
.
.
Now all you have to do is to select for b some base that you can work in easily. For example,
let b = 10. Substituting this into the formula that is being derived results in:
.
.
Now use a calculator to find that  and 
.
Substitute those values into the formula and it becomes:
.
.
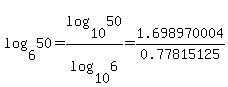
Do the division and the result is:
.
.
And that is typical of using the change of base formula to find logs to other bases.
.
Hope this helps you to understand the change of base formula.
.
|
|
|
