Question 1203862: you have 400,000 saved for retirement. your account earns 8% interest. how much will you be able to pull out each month if you want to be able to take withdrawals for 15 years
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! monthly compounding is assumed.
calculator used is at https://arachnoid.com/finance/
results are shown below:
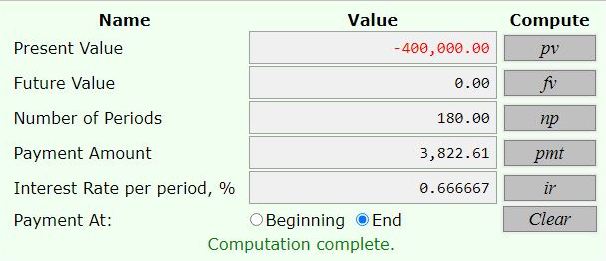
present value is set to -400,000.
interest rate per time period = 8% per year / 12 = .66666666....% per month.
number of time periods = 15 years * 12 = 180 months.
payments are withdrawn at the end of each month.
investment is assumed to be made 1 month prior to when the first withdrawal is desired.
calculator says that 3,822.61 is able to be withdrawn at the end of each month.
Answer by ikleyn(52750)  (Show Source):
You can put this solution on YOUR website! .
you have 400,000 saved for retirement. your account earns 8% interest.
how much will you be able to pull out each month if you want to be able
to take withdrawals for 15 years
~~~~~~~~~~~~~~~~~
In such problems, people usually withdraw money at the beginning of a month
for living - not at the end of the month.
So, I made my own calculations to account for this factor (in @Theo solution
withdrawals were made at the end of each month).
In my solution, withdrawals are made at the beginning of the month.
Use the general formula A =  .
Here A is the initial amount at the account; W is the monthly withdrawn value;
r is the nominal monthly percentage r = 0.08/12 presented as a decimal;
p = 1 + r and n is the number of withdrawing periods (months, in this case).
In this problem, W is the unknown; the monthly rate is r = 0.08/12 = 0.006666667,
p = 1 + 0.006666667 = 1.006666667, the number of payment periods (= the number of months) is n = 15*12 = 180.
So
400000 =  .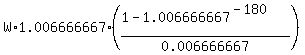
The factor 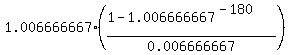 is equal to 105.3381936; therefore
W =  = 3797.29 dollars (rounded to the closest lesser cent).
Thus you will be able to withdraw about $3797.293141 every month during 15 years..
Solved.
--------------------
In this site, there is a group of lessons associated with annuity saving plans and retirement plans. They are
- Ordinary Annuity saving plans and geometric progressions
- Annuity Due saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
- Withdrawing a certain amount of money periodically from a compounded saving account (*)
- Miscellaneous problems on retirement plans
From these lessons, you can learn the subject and can see many similar solved problems.
The closest lesson to your problem is marked (*) in the list.
\\\\\\\\\\\\\\\\\\\\\\\\
To make such complicated calculations as they are in this problem,
you should have/use an appropriate calculator for such long formulas.
Ideal choice is MS Excel, if you have it in your computer.
Then you write a formula in a text editor, copy-paste it
into an Excel work-sheet cell and click "Enter" - the result is ready
in the next second.
If you have no MS Excel in your computer, you may find similar
free of charge calculators in the Internet. One such calculator is
www.desmos.com/calculator
It allows you to do the same thing: you write a formula in a text editor,
copy-paste it into this calculator and click "Enter" - the result is ready
in the next instance.
|
|
|
