SOLUTION: Describe the transformation on the following graph of f(x) = log(x). State the placement of the horizontal asymptote and x-intercept after the transformation. For example, "left 1"

These two don't have HORIZONTAL asymptotes, but they have do have VERTICAL
asymptotes.

Here are all the rules you'll ever need for such problems. There are 10 of 
them:

1. When +k is added to the right side of f(x), the graph of the new function
g(x) is the graph of f(x) shifted "UP k".

2. When -k is added to the right side of f(x), the graph of the new function
g(x) is the graph of f(x) shifted "DOWN k".

3. When x+k is substituted for x in the right side of f(x), the graph of the
new function g(x) is the graph of f(x) shifted "LEFT k".

4. When x-k is substituted for x in the right side of f(x), the graph of the
new function g(x) is the graph of f(x) shifted "RIGHT k".

5. When the right side of f(x) is multiplied by -1, the graph of the
new function g(x) is the graph of f(x) reflected into (or across) the x-axis

6. When -x is substituted for x in the right side of f(x), the graph of the
new function g(x) is the graph of f(x) reflected into (or across) the y-axis.

7. When the right side of f(x) is multiplied by k, where k > 1 the graph of 
the new function g(x) is the graph of f(x) stretched vertically by a factor 
of k.

8. When the right side of f(x) is multiplied by k, where k < 1 the graph of 
the new function g(x) is the graph of f(x) shrunk vertically by a factor 
of k.

9. When k is replaced by kx in the right side of f(x), where k > 1 the graph 
of the new function g(x) is the graph of f(x) shrunk horizontally by a factor
of k.

10. When k is replaced by kx in the right side of f(x), where k < 1 the graph
of the new function g(x) is the graph of f(x) stretched horizontally by a
factor of k.

(a)
For your first problem, we want to go from

f(x) = log(x)
 
to 

g(x) = log(x+2)

We see that the right side of g(x), which is log(x+2), is the result of
substituting x+2 for x in the right side of f(x), so by rule 3, the
graph of g(x) is the graph of f(x) shifted "LEFT 2"

Here is the graph of f(x) = log(x). Notice that the y-axis is the
vertical asymptote, and that the x-intercept is (1,0)



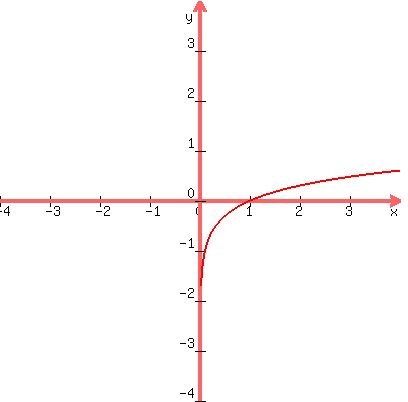And here is the graph of g(x) = log(x+2).  Note that the vertical
asymptote has been also shifted left by 2 units from x = 0 (the
y-axis) to x = -2. Notice also that the x-intercept has been
shifted left by 2 units from (1,0) to (-1,0). 



Here they are both on the same graph:



b) g(x) = -log(x)

For your second problem, we want to go from

f(x) = log(x)
 
to 

g(x) = -log(x)

We see that the right side of g(x), which is -log(x), is the result of
multiplying the right side of f(x) by -1, so by rule 5, the
graph of g(x) is the graph of f(x) reflected across the x-axis.

Here is the graph of f(x) = log(x) again



And here is the graph of g(x) = -log(x)



Here they are both on the same graph:



Notice that the vertical asymptote is the same for both
because a reflection across the x-axis of a vertical line
is the same vertical line.  Also notice that their 
x-intercepts are the same point (1,0).  Any point on
the x-axis remains the same when a graph is reflected
across the x-axis.

Edwin