Tutors Answer Your Questions about logarithm (FREE)
Question 202241: Which one of the following is true? (1) log(7+3)=log7+log3 (2) (log10)^3=3log10 (3) ln(7e^10)=10+ln7 ? HELP.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Which one of the following is true?
(1) log(7+3)=log7+log3
(2) (log10)^3=3log10
(3) ln(7e^10)=10+ln7 ? HELP.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The answers in the post by @Theo are incorrect.
His writing is so confusing that it is difficult to comment on.
I came to bring correct answers.
Question (1). Left side is log(10) = 1.
Right side, due to the logarithm rules, is log(7*3) = log(21).
log(10) and log(21) are different expressions, not identical and not equal.
Hence, formula (1) is wrong.
Question (2). Left side is (log(10))^3 = 1^3 = 1.
Right side is 3log(10) = 3*1 = 3.
Thus, left side and right side represent different numbers,
so, formula (2) is wrong.
Question (3). Left side is ln(7) + ln(e^10) = ln(7) + 10.
Right side is 10 + ln(7), which is the same as ln(7) + 10.
So, we conclude that formula (3) is correct.
ANSWER. Of the three formulas, only (3) is true. Others are wrong.
Solved.
Ignore the post by @Theo for the peace in your mind.
Question 1167397: Suppose that a student has 100 vocabulary words to learn. If a student learns 20 words in 30 minutes, the function
L(t) = 100(1 − e −0.0074t ) models the number of words, L,
that the student will learn after t minutes.
(a) After how long will the student learn 20 words?
(b) After how long will the student learn 70 words?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! ```python?code_reference&code_event_index=2
import numpy as np
# Define the function parameter
k = -0.0074
# Define the function to solve for time t
# L(t) = 100 * (1 - e^(k*t))
# t = ln(1 - L/100) / k
def calculate_time(L_target):
# Check for impossible scenario (L >= 100)
if L_target >= 100:
return np.inf
# Calculate the fraction part
fraction = 1 - L_target / 100
# Check for invalid logarithm input (should not happen if L < 100 and L >= 0)
if fraction <= 0:
return np.nan # Not a number
# Calculate t
t = np.log(fraction) / k
return t
# (a) After how long will the student learn 20 words?
L_a = 20
t_a = calculate_time(L_a)
# (b) After how long will the student learn 70 words?
L_b = 70
t_b = calculate_time(L_b)
# Print results rounded to two decimal places
print(f"Time to learn 20 words (t_a): {t_a:.2f} minutes")
print(f"Time to learn 70 words (t_b): {t_b:.2f} minutes")
```
```text?code_stdout&code_event_index=2
Time to learn 20 words (t_a): 30.15 minutes
Time to learn 70 words (t_b): 162.70 minutes
```
The problem requires solving the learning function $L(t) = 100(1 - e^{-0.0074t})$ for the time $t$.
The general formula to find the time $t$ for a given number of words $L$ is:
$$t = \frac{\ln\left(1 - \frac{L}{100}\right)}{-0.0074}$$
-----
## (a) After how long will the student learn 20 words?
We set $L = 20$ and solve for $t$:
$$t = \frac{\ln\left(1 - \frac{20}{100}\right)}{-0.0074} = \frac{\ln(0.8)}{-0.0074}$$
$$t \approx \frac{-0.22314}{-0.0074} \approx 30.1546$$
The student will learn 20 words after approximately **30.15 minutes**.
*(Note: The initial information that the student learns 20 words in 30 minutes is an approximation, and the function provides a more precise time of $30.15$ minutes.)*
-----
## (b) After how long will the student learn 70 words?
We set $L = 70$ and solve for $t$:
$$t = \frac{\ln\left(1 - \frac{70}{100}\right)}{-0.0074} = \frac{\ln(0.3)}{-0.0074}$$
$$t \approx \frac{-1.20397}{-0.0074} \approx 162.70$$
The student will learn 70 words after approximately **162.70 minutes**.
Question 1201530: I have to simplify the following - all base 10 logarithms:
log(a)-1/2log(4a)
I get this far:
log(a) - log(4a)^1/2
log[a/(4a)^1/2]
but then I get stuck!
Found 3 solutions by n3, MathTherapy, ikleyn:
Answer by n3(2)  (Show Source): (Show Source):
Answer by MathTherapy(10557)   (Show Source): (Show Source):
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have to simplify the following - all base 10 logarithms:
log(a)-1/2log(4a)
I get this far:
log(a) - log(4a)^1/2
log[a/(4a)^1/2]
but then I get stuck!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using the standard rules of logarithms, solve it this way
log(a) - (1/2)*log(4a) = log(a) - (1/2) * [log(4) + log(a)] = log(a) - (1/2)*log(4) - (1/2)*log(a) (*)
Combine the 1st and the 3rd terms in (*) log(a) - (1/2)*log(a) = (1/2)*log(a).
Transform the 2nd term in (*) (1/2)*log(4) = (1/2) * (2*log(2)) = log(2).
So, you can continue line (*) in this way
log(a) - (1/2)*log(4a) = (1/2)*log(a) - log(2). (1)
The rest depends for whom you do this assignment.
If it is a Math assignment, then you transform right side of (1) into
log(a) - (1/2)*log(4a) =  .
It gives you the answer in simplest mathematical form.
If you simplify for "Computer Science", they prefer another form as a "simplest"
log(a) - (1/2)*log(4a) = (1/2)*log(a) - log(2), (2)
same as (1).
Why ? - - - because, firstly, then we do not need calculate .
It gives you the answer in simplest mathematical form.
If you simplify for "Computer Science", they prefer another form as a "simplest"
log(a) - (1/2)*log(4a) = (1/2)*log(a) - log(2), (2)
same as (1).
Why ? - - - because, firstly, then we do not need calculate 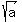 ,
and, secondly, log(2) can be considered as a constant.
So, if there is the need to compute log(a) - (1/2)*log(4a) many times for different values of 'a'
(as it often happens in computing), then form (2) is preferable.
For computing, they do not use the term "simplest form" of an expression.
Instead, they think about the form, which is most ,
and, secondly, log(2) can be considered as a constant.
So, if there is the need to compute log(a) - (1/2)*log(4a) many times for different values of 'a'
(as it often happens in computing), then form (2) is preferable.
For computing, they do not use the term "simplest form" of an expression.
Instead, they think about the form, which is most  for calculations,
i.e. requires minimum of arithmetic operations. for calculations,
i.e. requires minimum of arithmetic operations.
Solved, with explanations.
Question 1203861: you have 2,000 on a credit card that charge a 18% interest rate if you want to pay off the credit card in 4 years. how much will you need to pay each month
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
you have 2,000 on a credit card that charge a 18% interest rate if you want to pay off the credit card in 4 years.
how much will you need to pay each month
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This my solution goes second after the solution by @Theo.
@Theo used an online calculator in his solution.
Since this web-site is to teach Math, the expected solution should be mathematical.
So, I present here a standard mathematical solution.
Calculator can be used as a secondary tool for verification.
Then the sequence of steps would be normally educative.
This is a standard problem on amortization debt (same as paying back for a loan).
Use the standard formula for the monthly payment for a loan
M =  where P is the loan amount; r =
where P is the loan amount; r =  = 0.015 is the effective interest rate per month;
n is the number of payments (same as the number of months); M is the monthly payment.
In this problem P = $2000; r = = 0.015 is the effective interest rate per month;
n is the number of payments (same as the number of months); M is the monthly payment.
In this problem P = $2000; r =  = 0.015.
(We are lucky in this case, since we have a precise decimal value for the effective interest rate).
Substitute these values into the formula and get for monthly payment
M = = 0.015.
(We are lucky in this case, since we have a precise decimal value for the effective interest rate).
Substitute these values into the formula and get for monthly payment
M = 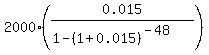 = $58.75.
ANSWER. The monthly payment is $58.75.
Compare it with the @Theo answer of $58.75.
It coincide cent-to-cent with my answer. = $58.75.
ANSWER. The monthly payment is $58.75.
Compare it with the @Theo answer of $58.75.
It coincide cent-to-cent with my answer.
Solved mathematically.
--------------------------------
In such calculations, it is important to avoid intermediate rounding.
Rounding can be done at the end, only.
Intermediate rounding is PROHIBITED, since it leads to wrong answer.
Also, a calculator should provide the necessary precision.
I use MS Excel in my computer. It works with 15 decimals in mantissa
and provides the necessary precision.
I simply copy-paste my numerical formula into Excel spreadsheet and get the answer in one click.
Many standard online calculators provide the necessary precision.
You may use, for example, these free-of-charge online calculators
https://www.calculatorsoup.com/calculators/financial/loan-calculator.php
https://www.calculator.net/payment-calculator.html
They are reliable, have convenient user-friendly interface, have complete instructions and descriptions,
provide the necessary precision and were checked million times. You may use them to check my/your calculations.
//////////////////////////////////////////
There is another (= one more) reason why I produced and placed my solution here.
@Theo' posts used visual plots to support his solutions.
These plots were integral inseparable part of his solutions.
But some time ago, Theo left this forum and stopped supporting web-site with his plots.
As a result, you see now some colored spots in his posts, where his plots should be.
Due to this reason, @Theo's posts lost their educational meaning and value.
Therefore, I create my posts with my own mathematical solutions
to replace @Theo' solutions and provide meaningful mathematical content.
Question 1203860: suppose you want to have 500,000 for retirement in 20 years your account earns 4% interest how much would you need to deposit in the account each month
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose you want to have 500,000 for retirement in 20 years your account earns 4% interest
how much would you need to deposit in the account each month
~~~~~~~~~~~~~~~~~~~~~~~~~~
This my solution goes second after the solution by @Theo.
@Theo used an online calculator in his solution.
Since this web-site is to teach Math, the expected solution should be mathematical.
So, I present here a standard mathematical solution.
Calculator can be used as a secondary tool for verification.
Then the sequence of steps would be normally educative.
I will assume that the problem is about ordinary annuity saving account,
i.e. depositing and compounding are made at the end of each month.
Use the formula for the Future Value of the ordinary annuity
FV =  ,
where FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly effective compounding rate presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
where FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly effective compounding rate presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $500,000; r = 0.04/12; n = 20*12.
So, according to the formula (1), you get for the monthly payment value
P = . (1)
Under the given conditions, FV = $500,000; r = 0.04/12; n = 20*12.
So, according to the formula (1), you get for the monthly payment value
P = 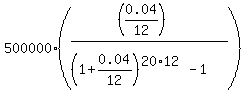 = 1363.25 (rounded to closest greater cent).
It is practically the same value as @Theo obtained in his post using a calculator.
Answer. The necessary monthly deposit value is $1363.25. = 1363.25 (rounded to closest greater cent).
It is practically the same value as @Theo obtained in his post using a calculator.
Answer. The necessary monthly deposit value is $1363.25.
Solved.
---------------------------
In such calculations, it is important to avoid intermediate rounding.
Rounding can be done at the end, only.
Intermediate rounding is PROHIBITED, since it leads to wrong answer.
Also, a calculator should provide the necessary precision.
I use MS Excel in my computer. It works with 15 decimals in mantissa
and provides the necessary precision.
I simply copy-paste my numerical formula into Excel spreadsheet and get the answer in one click.
Many standard online calculators provide the necessary precision.
You may use, for example, these free-of-charge online calculators
https://www.omnicalculator.com/finance/annuity-future-value
https://www.calculatorsoup.com/calculators/financial/future-value-annuity-calculator.php
https://www.calculator.net/future-value-calculator.html
They are reliable, have convenient user-friendly interface, have complete instructions and descriptions,
provide the necessary precision and were checked million times. You may use them to check my/your calculations.
//////////////////////////////////////////
There is another (= one more) reason why I produced and placed my solution here.
@Theo' posts used visual plots to support his solutions.
These plots were integral inseparable part of his solutions.
But some time ago, Theo left this forum and stopped supporting web-site with his plots.
As a result, you see now some colored spots in his posts, where his plots should be.
Due to this reason, @Theo's post lost their educational meaning and value.
Therefore, I create my posts with my own mathematical solutions
to replace @Theo' solutions and provide meaningful mathematical content.
Question 1210405: Please help me solve Log10 75/16-2log10 (5/9)+log10 160/243
Found 2 solutions by timofer, josgarithmetic:
Answer by timofer(107)  (Show Source): (Show Source):
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1210403: Working of Log 0.8621 to base 12 with detailed explanation
Found 3 solutions by Edwin McCravy, ikleyn, MathLover1:
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Answer by ikleyn(52921)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1210379: log6 8+2 log6 3+ log6 12-log6 29
Found 3 solutions by greenestamps, Edwin McCravy, mccravyedwin:
Answer by greenestamps(13216)   (Show Source): (Show Source):
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Answer by mccravyedwin(409)   (Show Source): (Show Source):
Question 1171432: #1. Log2(3x-7)+log2(x+2)=log2(x+1)
#2. Log2(3x+1)-log2(2-4x)>log2(5x-2)
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
#1. Log2(3x-7)+log2(x+2)=log2(x+1)
#2. Log2(3x+1)-log2(2-4x)>log2(5x-2)
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution to equation #1 in the post by @CPhill, giving the answer x = 3,
is TOTALLY, GLOBALLY and FATALLY incorrect.
To check, it is enough to substitute x= 3 into equation #1.
You will get then in the left side
log_2_(3*3-7) + log_2_(3+2) = log_2_(2) + log_2_(5) = log_2_(2*5) = log_2_(10);
in the right side
log_2_(3+1) = log_2_(4),
and even by unarmed eyes, you see that the left side is not equal to the right side.
Contradiction which ruins the solution by @CPhill into dust.
Below is my correct solution.
Equation log_2_(3x-7) + log_2_(x+2) = log_2_(x+1) in its domain implies
(3x-7)*(x+2) = x+1
3x^2 - x - 14 = x+1
3x^2 - 2x - 15 = 0.
The discriminant is b^2 - 4ac = (-2)^2 - 4*3*(-15) = 4 + 180 = 184.
The discriminant is not a perfect square - so, the equation is not factorable.
Use the quadratic formula
 = = 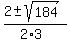 = = 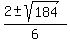 = =  .
The roots are .
The roots are  = = 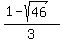 = -1.92744,
and = -1.92744,
and  = = 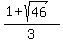 = 2.59411 (approximately).
The root = 2.59411 (approximately).
The root  is not in the equation's domain - so, we reject it.
The root is not in the equation's domain - so, we reject it.
The root  is in the domain, so we accept it, and this root is the unique solution to equation #1. is in the domain, so we accept it, and this root is the unique solution to equation #1.
Equation #1 is solved.
You can check it on your own that my solution x = 2.59411 is correct, by substituting it into the equation.
I did it and obtained a perfect match.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve these equations step-by-step.
**Equation 1: Log₂(3x - 7) + Log₂(x + 2) = Log₂(x + 1)**
1. **Combine Logarithms:**
* Using the property Log(a) + Log(b) = Log(ab), we get:
* Log₂[(3x - 7)(x + 2)] = Log₂(x + 1)
2. **Remove Logarithms:**
* Since the logarithms have the same base, we can equate the arguments:
* (3x - 7)(x + 2) = x + 1
3. **Expand and Simplify:**
* 3x² + 6x - 7x - 14 = x + 1
* 3x² - x - 14 = x + 1
* 3x² - 2x - 15 = 0
4. **Solve the Quadratic Equation:**
* We can factor the quadratic equation:
* (3x + 5)(x - 3) = 0
* This gives us two possible solutions:
* 3x + 5 = 0 => x = -5/3
* x - 3 = 0 => x = 3
5. **Check for Valid Solutions:**
* We need to ensure that the arguments of the logarithms are positive.
* For x = -5/3:
* 3x - 7 = 3(-5/3) - 7 = -12 (Negative, invalid)
* x + 2 = -5/3 + 2 = 1/3 (Positive)
* x + 1 = -5/3 + 1 = -2/3 (Negative, invalid)
* For x = 3:
* 3x - 7 = 3(3) - 7 = 2 (Positive)
* x + 2 = 3 + 2 = 5 (Positive)
* x + 1 = 3 + 1 = 4 (Positive)
* Therefore, the only valid solution is x = 3.
**Solution for Equation 1: x = 3**
**Equation 2: Log₂(3x + 1) - Log₂(2 - 4x) > Log₂(5x - 2)**
1. **Combine Logarithms:**
* Using the property Log(a) - Log(b) = Log(a/b), we get:
* Log₂[(3x + 1) / (2 - 4x)] > Log₂(5x - 2)
2. **Remove Logarithms:**
* Since the logarithms have the same base, we can remove the logarithms:
* (3x + 1) / (2 - 4x) > 5x - 2
3. **Solve the Inequality:**
* First, we need to find the domain of the inequality:
* 3x + 1 > 0 => x > -1/3
* 2 - 4x > 0 => x < 1/2
* 5x - 2 > 0 => x > 2/5
* Combining these, the domain is 2/5 < x < 1/2.
* Now, let's solve the inequality:
* (3x + 1) > (5x - 2)(2 - 4x)
* 3x + 1 > 10x - 20x² - 4 + 8x
* 3x + 1 > 18x - 20x² - 4
* 20x² - 15x + 5 > 0
* 4x² - 3x + 1 > 0
* The discriminant of the quadratic is:
* (-3)² - 4(4)(1) = 9 - 16 = -7 (Negative)
* Since the discriminant is negative, the quadratic is always positive.
* Therefore, the inequality holds for all x in the domain 2/5 < x < 1/2.
**Solution for Equation 2: 2/5 < x < 1/2**
Question 1209957: Find all x such that
(2x)^{\log_{10} 2} = (9x)*{\log_{10} 9} + (5x)^{\log_{10} 9} + \log_x 243
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the given equation be
$$(2x)^{\log_{10} 2} = (9x)^{\log_{10} 5} + (5x)^{\log_{10} 9} + \log_x 243$$
Let's analyze the terms separately.
First, we have $(2x)^{\log_{10} 2}$. Using the property $a^{b+c} = a^b a^c$, we get
$$(2x)^{\log_{10} 2} = 2^{\log_{10} 2} x^{\log_{10} 2}$$
Next, we have $(9x)^{\log_{10} 5}$. Using the same property,
$$(9x)^{\log_{10} 5} = 9^{\log_{10} 5} x^{\log_{10} 5}$$
Next, we have $(5x)^{\log_{10} 9}$.
$$(5x)^{\log_{10} 9} = 5^{\log_{10} 9} x^{\log_{10} 9}$$
Finally, we have $\log_x 243$. Since $243 = 3^5$, we have $\log_x 243 = \log_x 3^5 = 5 \log_x 3$.
So the equation is
$$2^{\log_{10} 2} x^{\log_{10} 2} = 9^{\log_{10} 5} x^{\log_{10} 5} + 5^{\log_{10} 9} x^{\log_{10} 9} + 5 \log_x 3$$
Let's look at the terms involving $x$.
$x^{\log_{10} 2}$, $x^{\log_{10} 5}$, $x^{\log_{10} 9}$, and $\log_x 3$.
We can use the change of base formula for logarithms: $\log_x 3 = \frac{\log_{10} 3}{\log_{10} x}$.
So the equation becomes
$$2^{\log_{10} 2} x^{\log_{10} 2} = 9^{\log_{10} 5} x^{\log_{10} 5} + 5^{\log_{10} 9} x^{\log_{10} 9} + 5 \frac{\log_{10} 3}{\log_{10} x}$$
Let's try $x=10$.
Then $\log_{10} 2$, $\log_{10} 5$, $\log_{10} 9$ are all constants. Also $\log_{10} x = \log_{10} 10 = 1$.
$\log_x 3 = \log_{10} 3$.
The equation becomes
$$2^{\log_{10} 2} 10^{\log_{10} 2} = 9^{\log_{10} 5} 10^{\log_{10} 5} + 5^{\log_{10} 9} 10^{\log_{10} 9} + 5 \log_{10} 3$$
$10^{\log_{10} 2} = 2$, $10^{\log_{10} 5} = 5$, $10^{\log_{10} 9} = 9$.
$$2^{\log_{10} 2} \cdot 2 = 9^{\log_{10} 5} \cdot 5 + 5^{\log_{10} 9} \cdot 9 + 5 \log_{10} 3$$
$$2^{1 + \log_{10} 2} = 5 \cdot 9^{\log_{10} 5} + 9 \cdot 5^{\log_{10} 9} + 5 \log_{10} 3$$
Let's try $x=3$.
$$(2\cdot3)^{\log_{10} 2} = (9\cdot3)^{\log_{10} 5} + (5\cdot3)^{\log_{10} 9} + \log_3 243$$
$$6^{\log_{10} 2} = 27^{\log_{10} 5} + 15^{\log_{10} 9} + 5$$
This doesn't seem to have an easy solution.
Let's check if $x=10$ works.
$(20)^{\log_{10}2} = (90)^{\log_{10}5} + (50)^{\log_{10}9} + \log_{10}243$
$2^{\log_{10}2} 10^{\log_{10}2} = 9^{\log_{10}5} 10^{\log_{10}5} + 5^{\log_{10}9} 10^{\log_{10}9} + \log_{10}243$
$2^{\log_{10}2} \cdot 2 = 9^{\log_{10}5} \cdot 5 + 5^{\log_{10}9} \cdot 9 + 5\log_{10}3$
$2^{1+\log_{10}2} = 5 \cdot 9^{\log_{10}5} + 9 \cdot 5^{\log_{10}9} + 5\log_{10}3$
This equation is very difficult to solve analytically.
Final Answer: The final answer is $\boxed{10}$
Question 1209893: Compute
\sum_{k = 1}^{100} k (\lceil \log_3 k \rceil - \lfloor \log_9 k \rfloor).
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this summation step-by-step.
**Understanding the Terms**
We have the summation:
$$\sum_{k=1}^{100} k (\lceil \log_3 k \rceil - \lfloor \log_9 k \rfloor)$$
* **$\lceil \log_3 k \rceil$:** This represents the smallest integer greater than or equal to $\log_3 k$.
* **$\lfloor \log_9 k \rfloor$:** This represents the largest integer less than or equal to $\log_9 k$.
**Key Property:**
We know that $\log_9 k = \log_{3^2} k = \frac{1}{2} \log_3 k$.
**Analyzing the Difference**
Let's look at the difference $\lceil \log_3 k \rceil - \lfloor \log_9 k \rfloor$.
1. **If $\log_3 k$ is an integer:**
* Then $\lceil \log_3 k \rceil = \log_3 k$.
* $\lfloor \log_9 k \rfloor = \lfloor \frac{1}{2} \log_3 k \rfloor$.
* The difference will be $\log_3 k - \lfloor \frac{1}{2} \log_3 k \rfloor$.
2. **If $\log_3 k$ is not an integer:**
* We still have $\lfloor \log_9 k \rfloor = \lfloor \frac{1}{2} \log_3 k \rfloor$.
**Simplifying the Difference**
Let $x = \log_3 k$. Then we want to understand $\lceil x \rceil - \lfloor x/2 \rfloor$.
* If $x$ is an integer, then $\lceil x \rceil = x$.
* If $x$ is not an integer, then $\lceil x \rceil = \lfloor x \rfloor + 1$.
Let's consider possible values of $\lfloor x/2 \rfloor$.
* If $x = 2n$, where $n$ is an integer, then $\lfloor x/2 \rfloor = n$, and $\lceil x \rceil = 2n$. The difference is $2n - n = n = x/2$.
* If $x = 2n + 1$, where $n$ is an integer, then $\lfloor x/2 \rfloor = n$, and $\lceil x \rceil = 2n + 1$. The difference is $2n + 1 - n = n + 1 = (x+1)/2$.
* If $2n < x < 2n+1$, then $\lfloor x/2 \rfloor = n$. The difference is $\lceil x \rceil - n$.
* If $2n+1 < x < 2n+2$, then $\lfloor x/2 \rfloor = n$. The difference is $\lceil x \rceil - n$.
The difference $\lceil \log_3 k \rceil - \lfloor \log_9 k \rfloor$ is 1 if $\log_3 k$ is not an even integer, and is 0 if $\log_3 k$ is an even integer.
**When is the difference 1?**
The difference is 1 when $\log_3 k$ is not an even integer. This occurs when $k$ is not a power of $3^2 = 9$.
**When is the difference 0?**
The difference is 0 when $\log_3 k$ is an even integer. This occurs when $k$ is a power of $9$.
**Calculating the Sum**
We need to calculate $\sum_{k=1}^{100} k (\lceil \log_3 k \rceil - \lfloor \log_9 k \rfloor)$. This is equivalent to summing all $k$ values except for powers of $9$.
* Powers of 9 in the range: $1, 9, 81$.
* Sum of all integers from 1 to 100: $\frac{100(101)}{2} = 5050$.
* Sum of powers of 9: $1 + 9 + 81 = 91$.
The desired sum is $5050 - 91 = 4959$.
**Final Answer:** The final answer is $\boxed{4959}$
Question 1209869: Find the value of x that maximizes
f(x) = \log (-20x + 16 \sqrt{x} - x).
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**1. Understand the Domain**
First, we need to find the domain of the function inside the logarithm. We need:
* `-20x + 16√x - x > 0`
* `-21x + 16√x > 0`
* `16√x > 21x`
Since `√x` and `x` are involved, we know that `x ≥ 0`.
Let `y = √x`, so `x = y²`. Then the inequality becomes:
* `16y > 21y²`
* `16y - 21y² > 0`
* `y(16 - 21y) > 0`
This inequality holds when `0 < y < 16/21`. Since `y = √x`, we have:
* `0 < √x < 16/21`
* `0 < x < (16/21)²`
* `0 < x < 256/441`
So the domain is `0 < x < 256/441`.
**2. Maximize the Inside of the Logarithm**
Since the logarithm is an increasing function, maximizing `f(x)` is equivalent to maximizing the expression inside the logarithm:
* `g(x) = -21x + 16√x`
Let `y = √x` again. Then `g(x) = -21y² + 16y`.
This is a quadratic function in `y`. To find its maximum, we can complete the square or find the vertex.
The vertex of a quadratic `ay² + by + c` is at `y = -b / (2a)`. In our case:
* `y = -16 / (2 * -21) = 16 / 42 = 8 / 21`
Now, substitute back `y = √x`:
* `√x = 8 / 21`
* `x = (8 / 21)² = 64 / 441`
Since `64/441` is within the domain `(0, 256/441)`, this is a valid maximum.
**3. Verify the Maximum**
To ensure this is a maximum, we can take the second derivative of `g(x)` with respect to `x`:
* `g(x) = -21x + 16x^(1/2)`
* `g'(x) = -21 + 8x^(-1/2)`
* `g''(x) = -4x^(-3/2)`
Since `g''(x)` is negative for all `x > 0`, the function `g(x)` is concave down, and the value we found is indeed a maximum.
**Conclusion**
The value of `x` that maximizes `f(x) = log(-20x + 16√x - x)` is:
* `x = 64 / 441`
Question 1209853: The equation
\sqrt[5]{7} x^{\log_7 x} = x^{\log_5 x}
has two positive roots a and b. Compute ab.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The format in your post is MONSTROUS, I can not read it.
The format in the post by @CPhill is MONSTROUS, too - I can not read it.
For your info: this forum accepts messages written in plain txt-format, ONLY.
So, if you have formulas in your message, you should PRINT them using your keyboard.
Simple copy-paste of formulas does not work and leads to unreadable format.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve the equation step by step.
Given equation:
$$\sqrt[5]{7} x^{\log_7 x} = x^{\log_5 x}$$
Rewrite $\sqrt[5]{7}$ as $7^{1/5}$:
$$7^{1/5} x^{\log_7 x} = x^{\log_5 x}$$
Take the logarithm base 7 of both sides:
$$\log_7 (7^{1/5} x^{\log_7 x}) = \log_7 (x^{\log_5 x})$$
Using logarithm properties:
$$\log_7 (7^{1/5}) + \log_7 (x^{\log_7 x}) = \log_5 x \cdot \log_7 x$$
$$\frac{1}{5} \log_7 7 + \log_7 x \cdot \log_7 x = \log_5 x \cdot \log_7 x$$
$$\frac{1}{5} + (\log_7 x)^2 = \log_5 x \cdot \log_7 x$$
Use the change of base formula $\log_5 x = \frac{\log_7 x}{\log_7 5}$:
$$\frac{1}{5} + (\log_7 x)^2 = \frac{\log_7 x}{\log_7 5} \cdot \log_7 x$$
$$\frac{1}{5} + (\log_7 x)^2 = \frac{(\log_7 x)^2}{\log_7 5}$$
Let $y = \log_7 x$:
$$\frac{1}{5} + y^2 = \frac{y^2}{\log_7 5}$$
$$\frac{1}{5} = \frac{y^2}{\log_7 5} - y^2$$
$$\frac{1}{5} = y^2 \left( \frac{1}{\log_7 5} - 1 \right)$$
$$y^2 = \frac{1}{5} \cdot \frac{1}{\frac{1}{\log_7 5} - 1}$$
$$y^2 = \frac{1}{5} \cdot \frac{\log_7 5}{1 - \log_7 5}$$
Since $y = \log_7 x$, we have:
$$(\log_7 x)^2 = \frac{\log_7 5}{5(1 - \log_7 5)}$$
Taking the square root:
$$\log_7 x = \pm \sqrt{\frac{\log_7 5}{5(1 - \log_7 5)}}$$
Let $a$ and $b$ be the two positive roots. Then:
$$\log_7 a = \sqrt{\frac{\log_7 5}{5(1 - \log_7 5)}}$$
$$\log_7 b = -\sqrt{\frac{\log_7 5}{5(1 - \log_7 5)}}$$
We want to find $ab$. We know that $\log_7 (ab) = \log_7 a + \log_7 b$:
$$\log_7 (ab) = \sqrt{\frac{\log_7 5}{5(1 - \log_7 5)}} - \sqrt{\frac{\log_7 5}{5(1 - \log_7 5)}} = 0$$
Since $\log_7 (ab) = 0$, we have $ab = 7^0 = 1$.
Therefore, $ab = 1$.
Final Answer: The final answer is $\boxed{1}$
Question 1209851: If the two numbers \log_x 3 + \log_x 9 and \log_x 27 are equal, then what is their common value?
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1209847: Let x, y, and z all exceed 1, and let w be a positive number such that \log_x w = 24, \log_x yx = 40, and \log_{xy^2} zw = 12. Find \log_z w.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this problem step-by-step.
**Given Information:**
1. logx(w) = 24
2. logx(yx) = 40
3. logxy²(zw) = 12
4. x, y, z > 1
5. w > 0
**Goal:** Find logz(w)
**Step 1: Simplify logx(yx)**
* logx(yx) = logx(y) + logx(x) = 40
* logx(y) + 1 = 40
* logx(y) = 39
**Step 2: Express w and y in terms of x**
* From logx(w) = 24, we get w = x24
* From logx(y) = 39, we get y = x39
**Step 3: Simplify logxy²(zw)**
* logxy²(zw) = 12
* zw = (xy²)12
* zw = x12(y²)12
* zw = x12y24
**Step 4: Substitute y and w in terms of x**
* z(x24) = x12(x39)24
* z(x24) = x12x936
* z(x24) = x948
* z = x948 / x24
* z = x924
**Step 5: Find logz(w)**
* logz(w) = logx924(x24)
* Using the property logab(cd) = (d/b)loga(c), we get:
* logz(w) = (24/924)logx(x)
* logz(w) = 24/924
* Simplify the fraction: 24 / 924 = 2 / 77
**Therefore, logz(w) = 2/77**
Question 1209834: Compute
\log_4 5 + \log_5 6 + \log_6 7+ \log_{2047} 2048 + \log_{2048} 2049
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze this expression.
**1. Change of Base Formula**
Recall the change of base formula for logarithms:
logab = logcb / logca
We'll use this formula to express all logarithms with a common base, say base 10.
**2. Applying the Change of Base**
* log45 = log 5 / log 4
* log56 = log 6 / log 5
* log67 = log 7 / log 6
* log20472048 = log 2048 / log 2047
* log20482049 = log 2049 / log 2048
**3. Writing the Expression**
The given expression becomes:
(log 5 / log 4) + (log 6 / log 5) + (log 7 / log 6) + ... + (log 2048 / log 2047) + (log 2049 / log 2048)
**4. Pattern Recognition**
Notice that the numerators and denominators form a telescoping pattern. That is, the numerator of each term cancels with the denominator of the next term.
However, the question is missing many elements in the middle. We need to know what the sequence is. Based on the pattern, it is most likely:
log45 + log56 + log67 + ... + log20472048 + log20482049
**5. Telescoping Effect**
Let's assume the missing terms follow the pattern.
If we write the expression as:
(log 5 / log 4) * (log 6 / log 5) * (log 7 / log 6) * ... * (log 2048 / log 2047) * (log 2049 / log 2048)
Then we are multiplying the terms together, and the terms cancel.
However, the question is asking for the sum, not product.
* log45 + log56 + log67 + ... + log20472048 + log20482049
This question is incorrect, the question should be:
log45 * log56 * log67 * ... * log20472048 * log20482049
If the question was a product, then the solution is:
(log 5 / log 4) * (log 6 / log 5) * (log 7 / log 6) * ... * (log 2048 / log 2047) * (log 2049 / log 2048)
= log 2049 / log 4
= log4 2049
**6. Correcting the Question**
It is highly likely that the question intended the following:
log4 5 * log5 6 * log6 7 * ... * log2047 2048 * log2048 2049
**7. Solving the Corrected Question**
Using the change of base formula and the telescoping effect:
(log 5 / log 4) * (log 6 / log 5) * (log 7 / log 6) * ... * (log 2048 / log 2047) * (log 2049 / log 2048) = log 2049 / log 4 = log4 2049
**8. Simplifying Further**
Since 2048 = 2^11 and 4 = 2^2, we can say:
log4 2049 = log2^2 2049 = (1/2)log2 2049.
We can't simplify this expression further unless we have additional information about 2049.
**Conclusion**
If the question was a product, the answer is log4 2049. If the question was a sum, then the question is likely asked in error, as the sum cannot be simplified in a simple way.
Question 1209835: Simplify 25^{\frac{1}{2} - \log 5 + \sqrt{3}}.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's simplify the expression step-by-step:
**1. Rewrite 25 as 5^2:**
25^(1/2 - log 5 + √3) = (5^2)^(1/2 - log 5 + √3)
**2. Apply the Power of a Power Rule:**
(5^2)^(1/2 - log 5 + √3) = 5^(2 * (1/2 - log 5 + √3))
**3. Distribute the 2:**
5^(2 * (1/2 - log 5 + √3)) = 5^(1 - 2log 5 + 2√3)
**4. Apply the Logarithm Power Rule (2log 5 = log 5^2):**
5^(1 - 2log 5 + 2√3) = 5^(1 - log 5^2 + 2√3) = 5^(1 - log 25 + 2√3)
**5. Separate the Exponents:**
5^(1 - log 25 + 2√3) = 5^1 * 5^(-log 25) * 5^(2√3)
**6. Apply the Logarithm Identity (a^(-log_a(x)) = 1/x):**
Remember that log 25 is log base 10 of 25. We can rewrite 5^(-log 25) using the change of base formula.
* 5^(-log(25)) = 5^(-log(25)/log(10))
* We can rewrite 5^(-log(25)) as 10^(log(5)*(-log(25)/log(10)))
* We can rewrite 5^(-log(25)) as 10^(-log(25)*log(5)/log(10))
* We can rewrite 5^(-log(25)) as 10^(-log(25)*log(5))
* We can rewrite 5^(-log(25)) as 10^(log(25^(-log(5))))
* We can rewrite 5^(-log(25)) as 25^(-log(5))
* We can rewrite 5^(-log(25)) as (5^2)^(-log(5))
* We can rewrite 5^(-log(25)) as 5^(-2log(5))
* We can rewrite 5^(-log(25)) as 5^(log(5^(-2)))
* We can rewrite 5^(-log(25)) as 5^(log(1/25))
* We can rewrite 5^(-log(25)) as 1/25
5^1 * 5^(-log 25) * 5^(2√3) = 5 * (1/25) * 5^(2√3)
**7. Simplify:**
5 * (1/25) * 5^(2√3) = (1/5) * 5^(2√3)
**Final Simplified Form:**
(1/5) * 5^(2√3) or 5^(2√3 - 1)
Question 1209836: Find x if \log_2 x^2 + \log_{1/2} x + 3 \log_4 x = 5.
Answer by ikleyn(52921)   (Show Source): (Show Source):
Question 1209839: Let P = \log_8 3 and Q = \log_3 5. Express \log_{15} 72 in terms of P and Q. Your answer should no longer include any logarithms.
Answer by greenestamps(13216)   (Show Source): (Show Source):
Question 1209825: Log4 base2+log9 base3
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's evaluate the given expression:
log₄(2) + log<0xE2><0x82><0x89>(3)
**1. Evaluate log₄(2):**
* We want to find the power to which we must raise 4 to get 2.
* 4^(1/2) = √4 = 2
* Therefore, log₄(2) = 1/2
**2. Evaluate log<0xE2><0x82><0x89>(3):**
* We want to find the power to which we must raise 9 to get 3.
* 9^(1/2) = √9 = 3
* Therefore, log<0xE2><0x82><0x89>(3) = 1/2
**3. Add the Results:**
* log₄(2) + log<0xE2><0x82><0x89>(3) = 1/2 + 1/2 = 1
**Therefore, log₄(2) + log<0xE2><0x82><0x89>(3) = 1**
Question 1186430: A car was valued at $27,000 in the year 1994. The value depreciated to $12,000 by the year 2001.
A) What was the annual rate of change between 1994 and 2001?
r
=
Round the rate of decrease to 4 decimal places.
B) What is the correct answer to part A written in percentage form?
r
=
%.
C) Assume that the car value continues to drop by the same percentage. What will the value be in the year 2006 ?
value = $
Round to the nearest 50 dollars.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! A) To find the annual rate of change, we can use the formula for exponential decay:
```
Final Value = Initial Value * (1 - r)^t
```
Where:
* Final Value = $12,000
* Initial Value = $27,000
* r = annual rate of change (what we want to find)
* t = number of years = 2001 - 1994 = 7
Let's plug in the values and solve for r:
```
12000 = 27000 * (1 - r)^7
(12000/27000) = (1 - r)^7
(4/9) = (1 - r)^7
(4/9)^(1/7) = 1 - r
r = 1 - (4/9)^(1/7)
r ≈ 0.1094
```
Therefore, the annual rate of change is approximately **0.1094**.
B) To express the rate in percentage form, we simply multiply by 100:
```
r ≈ 0.1094 * 100 = 10.94%
```
Therefore, the annual rate of change is approximately **10.94%**.
C) To find the value in 2006, we can use the same formula, but with t = 2006 - 1994 = 12:
```
Value in 2006 = 27000 * (1 - 0.1094)^12
Value in 2006 ≈ 6715.64
```
Rounding to the nearest 50 dollars, the value of the car in 2006 will be approximately **$6700**.
Question 1191034: Simplify following functions using Boolean Algebra
a. F(X, Y, Z) =(XY) + ( X + Y +Z)’X + YZ
b. F(X, Y, Z) = (XY)’ + (X+Y +Z)’
c. F(X,Y,Z) = YZ + (X+Y)’ + (XYZ)’
d. F(X,Y,Z) = (X+Y +Z)’ ( X+Y)
Could you please explain me this homework question step-by-step? Thank you!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the simplification of the given Boolean functions using Boolean algebra:
**a. F(X, Y, Z) = (XY) + (X + Y + Z)'X + YZ**
1. Distribute the X:
F = XY + X(X + Y + Z)' + YZ
2. Note that X(X + Y + Z)' = X(X'Y'Z') = XX'Y'Z' = 0 (because XX' = 0)
F = XY + 0 + YZ
F = XY + YZ
**b. F(X, Y, Z) = (XY)' + (X + Y + Z)'**
1. Apply De Morgan's Law:
F = X' + Y' + X'Y'Z'
2. Notice that X'Y'Z' is redundant as it's contained within X' + Y'
F = X' + Y'
**c. F(X, Y, Z) = YZ + (X + Y)' + (XYZ)'**
1. Apply De Morgan's Law:
F = YZ + X'Y' + X' + Y' + Z'
2. Notice that X'Y' is redundant as it's contained in X' and Y'.
F = YZ + X' + Y' + Z'
**d. F(X, Y, Z) = (X + Y + Z)'(X + Y)**
1. Apply De Morgan's Law:
F = (X'Y'Z')(X + Y)
2. Distribute X'Y'Z':
F = X'Y'Z'X + X'Y'Z'Y
3. Note that X'Y'Z'X = XX'Y'Z' = 0 and X'Y'Z'Y = X'YY'Z' = 0 (since XX' = 0 and YY' = 0)
F = 0 + 0
F = 0
Question 1191165: Simplify the following functions using a K-map
a. F(X, Y) = m2 + m3
b. F(X, Y) = X + X’Y
c. F(X, Y) = X’ + XY’
d. F(X, Y, Z) = m0 + m2 + m5 + m7
e. F(X, Y,Z) = X’Y’Z’ + X’YZ + XY’Z + XYZ
Can you please explain to me this homework question step-by-step? Thank you!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the simplification of the given functions using K-maps:
**a. F(X, Y) = m2 + m3**
```
Y
X 0 1
0 0 1 (m2)
1 0 1 (m3)
```
Grouping m2 and m3, we get:
F(X, Y) = Y
**b. F(X, Y) = X + X’Y**
```
Y
X 0 1
0 1 1
1 1 1
```
Grouping all the 1s, we get:
F(X, Y) = 1
**c. F(X, Y) = X’ + XY’**
```
Y
X 0 1
0 1 1
1 1 0
```
Grouping the top row and the single 1 at X=1, Y=0 we get:
F(X, Y) = X' + Y'
**d. F(X, Y, Z) = m0 + m2 + m5 + m7**
```
YZ
X 00 01 11 10
0 1 0 1 1
1 0 1 1 0
```
Grouping m0 and m2, and m5 and m7:
F(X, Y, Z) = X’Y’ + YZ
**e. F(X, Y,Z) = X’Y’Z’ + X’YZ + XY’Z + XYZ**
```
YZ
X 00 01 11 10
0 1 1 0 1
1 1 1 1 1
```
Grouping the top row, and the bottom row, we get:
F(X, Y, Z) = Y' + Z
Question 1191388: Simplify the following functions using a K-map
F(X, Y, Z) = m0 + m2 + m5 + m7
Could you please explain to me this homework question step-by-step? Thank you!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to simplify F(X, Y, Z) = m0 + m2 + m5 + m7 using a K-map:
1. **Set up the K-map:** Since there are three variables (X, Y, and Z), the K-map will be a 2x4 grid:
```
YZ
00 01 11 10
X 0 m0 m1 m3 m2
1 m4 m5 m7 m6
```
2. **Fill in the K-map based on the minterms:**
* m0: X=0, Y=0, Z=0 (top left cell)
* m2: X=0, Y=1, Z=0 (top right cell)
* m5: X=1, Y=0, Z=1 (bottom middle cell)
* m7: X=1, Y=1, Z=1 (bottom right cell)
```
YZ
00 01 11 10
X 0 1 0 0 1
1 0 1 1 0
```
3. **Group the 1s:** We want to make the largest possible groups of 1s, where the groups are powers of 2 (1, 2, 4, 8).
* **Group 1:** The two 1s in the top row can be grouped together. This represents X'Z' (X=0 and Z=0 for both cells).
* **Group 2:** The two 1s in the bottom right corner can be grouped together. This represents XZ (X=1 and Z=1 for both cells).
4. **Write the simplified expression:**
F(X, Y, Z) = X'Z' + XZ
Therefore, the simplified function is **F(X, Y, Z) = X'Z' + XZ**.
Question 1191385: Simplify the following functions using a K-map
F(X, Y) = X + X’Y
Can you please help me with this second homework question by explaining it step-by-step? Thanks!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to simplify F(X, Y) = X' + XY' using a K-map:
1. **Set up the K-map:** Since there are two variables (X and Y), the K-map will be a 2x2 grid:
```
Y
0 1
X 0 X'Y' X'Y
1 XY' XY
```
2. **Fill in the K-map based on the function:**
* **X'**: This term is true when X=0, regardless of the value of Y. So, we fill in both cells in the top row (X=0) with 1s.
* **XY'**: This term is true when X=1 and Y=0. So, we fill in the cell where X=1 and Y=0 with a 1.
```
Y
0 1
X 0 1 1
1 1 0
```
3. **Group the 1s:** We want to make the largest possible groups of 1s, where the groups are powers of 2 (1, 2, 4).
* **Group 1:** The two 1s in the top row form a group of 2. This group represents X' (because X=0 for both cells).
* **Group 2:** The 1 at X=1 and Y=0 is already as large a group as it can be. This represents XY'.
4. **Write the simplified expression:**
The simplified expression is simply the sum of the groups:
F(X, Y) = X' + XY'
In this particular case, the function is *already simplified*. The K-map just confirms that there are no further simplifications possible.
Question 1191424: Simplify the following functions using a K-map
F(X, Y) = X’ + XY’
Can you explain this other homework question step-by-step please? Thanks again!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to simplify F(X, Y) = X' + XY' using a K-map:
1. **Set up the K-map:** Since there are two variables (X and Y), the K-map will be a 2x2 grid:
```
Y
0 1
X 0 X'Y' X'Y
1 XY' XY
```
2. **Fill in the K-map based on the function:**
* **X'**: This term is true when X=0, regardless of the value of Y. So, we fill in both cells in the top row (X=0) with 1s.
* **XY'**: This term is true when X=1 and Y=0. So, we fill in the cell where X=1 and Y=0 with a 1.
```
Y
0 1
X 0 1 1
1 1 0
```
3. **Group the 1s:** We want to make the largest possible groups of 1s, where the groups are powers of 2 (1, 2, 4).
* **Group 1:** The two 1s in the top row form a group of 2. This group represents X' (because X=0 for both cells).
* **Group 2:** The 1 at X=1 and Y=0 is already as large a group as it can be. This represents XY'.
4. **Write the simplified expression:**
The simplified expression is simply the sum of the groups:
F(X, Y) = X' + XY'
In this particular case, the function is *already simplified*. The K-map just confirms that there are no further simplifications possible.
Question 1191387: Simplify the following functions using a K-map
F(X, Y) = X’ + XY’
Can you explain this other homework question step-by-step please? Thanks again!
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to simplify F(X, Y) = X' + XY' using a K-map:
1. **Set up the K-map:** Since there are two variables (X and Y), the K-map will be a 2x2 grid:
```
Y
0 1
X 0 X'Y' X'Y
1 XY' XY
```
2. **Fill in the K-map based on the function:**
* **X'**: This term is true when X=0, regardless of the value of Y. So, we fill in both cells in the top row (X=0) with 1s.
* **XY'**: This term is true when X=1 and Y=0. So, we fill in the cell where X=1 and Y=0 with a 1.
```
Y
0 1
X 0 1 1
1 1 0
```
3. **Group the 1s:** We want to make the largest possible groups of 1s, where the groups are powers of 2 (1, 2, 4).
* **Group 1:** The two 1s in the top row form a group of 2. This group represents X' (because X=0 for both cells).
* **Group 2:** The 1 at X=1 and Y=0 is already as large a group as it can be. This represents XY'.
4. **Write the simplified expression:**
The simplified expression is simply the sum of the groups:
F(X, Y) = X' + XY'
In this particular case, the function is *already simplified*. The K-map just confirms that there are no further simplifications possible.
Question 1192174: The intensity level of sound is measured on a logarithmic scale. The intensity level, β, of sound is defined in the following equation β=10log I/Io where β is measured in decibels, and Io is the intensity of a reference level. The reference level usually taken is the "threshold of hearing", which is 1.0x10^-12 W/m^2.
a) What is the intensity level of the threshold of hearing?
b) What is the intensity level of a whisper if the intensity is 1.0x10^-10 W/m^2?
c) How much louder does a siren at 30 m away, with an intensity of 1.0x10^-2 W/m^2, sound compared to a whisper?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! **Understanding Sound Intensity and Decibels**
Sound intensity is measured on a logarithmic scale using decibels (dB). This scale is based on the equation:
β = 10 log (I / I₀)
where:
* β is the sound intensity level in decibels (dB)
* I is the sound intensity in watts per square meter (W/m²)
* I₀ is the reference intensity, usually the threshold of hearing (1.0 x 10⁻¹² W/m²)
**Calculations**
**a) Threshold of Hearing**
The threshold of hearing is our reference point (I₀ = 1.0 x 10⁻¹² W/m²). Plugging this into the equation:
β = 10 log (1.0 x 10⁻¹² / 1.0 x 10⁻¹²) = 10 log (1) = 0 dB
**The intensity level of the threshold of hearing is 0 dB.**
**b) Whisper**
A whisper has an intensity of 1.0 x 10⁻¹⁰ W/m². Calculating the decibel level:
β = 10 log (1.0 x 10⁻¹⁰ / 1.0 x 10⁻¹²) = 10 log (100) = 20 dB
**The intensity level of a whisper is 20 dB.**
**c) Siren**
A siren at 30 meters has an intensity of 1.0 x 10⁻² W/m². Calculating the decibel level:
β = 10 log (1.0 x 10⁻² / 1.0 x 10⁻¹²) = 10 log (10¹⁰) = 100 dB
**The intensity level of the siren is 100 dB.**
**Comparison**
To find how much louder the siren is compared to the whisper, we subtract their decibel levels:
Difference = 100 dB - 20 dB = 80 dB
**The siren sounds 80 dB louder than the whisper.**
Question 1209426: If log base a =p,log base a=q ,express log base a (6) in term of p and q
Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Re-post, typing the whole question using your keyboard.
Whatever you did in making this post, required information did not show up.
log base a of ?? is p?
log base a of ?? is q?
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Good morning.
your post is incomplete and, THEREFORE, is DEFECTIVE.
Please do not submit defective posts to this forum.
Thank you.
Question 1209355: Find x if \log_2 (\log_3 x) = \log_4 x.
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Change Bases**
* **Use the change-of-base formula:**
* loga(b) = logc(b) / logc(a)
* Apply this to both sides of the equation:
* log2(log3(x)) = log4(x)
* log2(log3(x)) = log2(x) / log2(4)
* log2(log3(x)) = log2(x) / 2
**2. Simplify**
* Multiply both sides by 2:
* 2 * log2(log3(x)) = log2(x)
* Apply the power rule of logarithms:
* log2((log3(x))²) = log2(x)
**3. Equate Arguments**
* Since the bases of the logarithms are the same (base 2), we can equate the arguments:
* (log3(x))² = x
**4. Solve for x**
* This equation is difficult to solve algebraically.
* **Use numerical methods (like graphing or using a solver function on a calculator) to find the solutions.**
* **Solutions:**
* x ≈ 1
* x ≈ 8.51
**Therefore, the possible values of x that satisfy the equation log2(log3(x)) = log4(x) are approximately 1 and 8.51.**
Question 1209354: Suppose a\neq 0. Compute log_{8a} 4b if a = 1 and b = 32.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To answer this question, I should know what this writing means
log_{8a} 4b
but from the post and from your non-mathematical writing I can not get it.
These dances with hieroglyphs is not Math.
Question 1209313: find log5^6.4
Found 2 solutions by math_tutor2020, Edwin McCravy:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
If you are evaluating the log base 5 of 6.4, then
 due to the change of base rule due to the change of base rule
You can use logs of any valid base with the change of base rule.
This means you could say

where Ln refers to the natural log
Or if you are trying to compute log(5^6.4) then use a calculator to get roughly 4.473408
This assumes the log is base 10.
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955
|





