SOLUTION: Evaluate sqrt(y/x) where x and y are positive integers, and 0=x^5-(x^3y^3)-12393

Your starting equation is

    x^5 - x^3*y^3 = 12393,      (1)

or

    x^3*(x^2 - y^3) = 12393.    (2)


Integer number 12393 has the primary decomposition  12393 = ,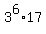  
so the last equation is

    x^3*(x^2 - y^3) = 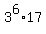.   (3)


From it, it is clear that for x, y to be integer solutions to this equation, it is necessary that x be 1, or 3, or 3^2 = 9.


So, we should consider these three cases.


(a)  x = 1.  Then from equation (3)

     x^2 - y^3 = 3^6*17 = 12393,  y^3 = 1 - 12393 = -12392.

                                  But this number is not a positive perfect cube, so this way does not work.



(b)  x = 3.  Then from equation (3)

     x^2 - y^3 = 3^3*17 = 459,  y^3 = 9 - 459 = -450. 

                                  But this number is not a positive perfect cube, so this way does not work.



(c)  x = 3^2 = 9.  Then from equation (3)

     x^2 - y^3 = 17,  y^3 = 81 - 17 = 64. 

                                 This number, 64, is a positive perfect cube, so  y = 4.


Thus, the solution to the given equation in this pair of positive integer numbers  (x,y) = (3,4).


Then 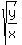   is this irrational number  =  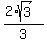= 1.154700538  (rounded).    ANSWER