SOLUTION: Show that the medians of two similar triangles are in the ratio the same as the ratio of their corresponding sides.

Algebra ->  Geometry-proofs -> SOLUTION: Show that the medians of two similar triangles are in the ratio the same as the ratio of their corresponding sides.      Log On


   

Question 999912: Show that the medians of two similar triangles are in the ratio the same as the ratio of their corresponding sides.
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
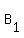
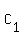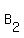
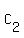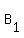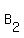Let two triangles  DELTAA%5B1%5DB%5B1%5DC%5B1%5D  and  DELTAA%5B2%5DB%5B2%5DC%5B2%5D  are similar,  so that the pairs of their corresponding sides  A%5B1%5DB%5B1%5D  and  A%5B2%5DB%5B2%5D, 

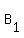
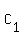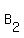
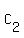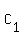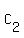 B%5B1%5DC%5B1%5D  and  B%5B2%5DC%5B2%5D,  and  A%5B1%5DC%5B1%5D  and  A%5B2%5DC%5B2%5D  are proportional with the same  (common)  coefficient of proportionality.

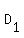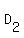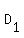
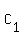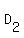
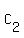Now consider two corresponding medians  A%5B1%5DD%5B1%5D  and  A%5B2%5DD%5B2%5D.  Consider the triangles  DELTAA%5B1%5DD%5B1%5DC%5B1%5D  and  DELTAA%5B2%5DD%5B2%5DC%5B2%5D. 

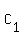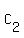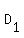
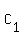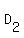
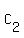They have two pairs of proportional sides  A%5B1%5DC%5B1%5D  and  A%5B2%5DC%5B2%5D,  D%5B1%5DC%5B1%5D  and  D%5B2%5DC%5B2%5D  with the same coefficient proportionality. 

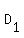
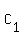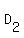
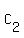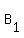
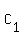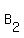
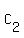For the last pair,  D%5B1%5DC%5B1%5D  and  D%5B2%5DC%5B2%5D,  it is true because these segments are halves of the corresponding sides  B%5B1%5DC%5B1%5D  and  B%5B2%5DC%5B2%5D.

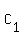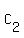The angles LC%5B1%5D and LC%5B2%5D  between these proportional sides are congruent,  as they are corresponding angles of the similar original triangles. 

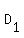
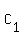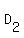
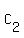Thus the triangles  DELTAA%5B1%5DD%5B1%5DC%5B1%5D  and  DELTAA%5B2%5DD%5B2%5DC%5B2%5D  have two pairs of proportional sides and the congruent angles between them. 

According to the  SAS-test of similarity for triangles,  these triangles are similar.

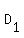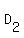Therefore,  their sides  A%5B1%5DD%5B1%5D  and  A%5B2%5DD%5B2%5D  are proportional with the same coefficient of proportionality. 

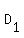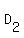It is exactly what has to be proved,  since  A%5B1%5DD%5B1%5D  and  A%5B2%5DD%5B2%5D  are the corresponding medians of the original triangles.