Question 999879: My daughter has a pre-algebra problem she nor I can figure out how to answer. The math problem is asking us to use the 5 step plan to solve it. Here is the written math problem to solve for:
What are the possible lengths and wideths of arectangle if its length is 8 centimeters longer than the width, and the area is less than or equal to 33 square centimeters?
a. Identify.
b. Strategize.
c. Set up.
d. Check.
We both came to the conclusion that since L x W = A that the Width must be 3 and the Length must be 11 because 11 x 3 = 33 since the problem states that the area must be less than or equal to 33 square cm. And since it states that the Length is 8 centimeters longer than the width we know that if 3 is the width then adding 8 to 3 = 11. Only problem is we do not understand how to set this up as an equation to solve through the 5 step plan. How do we do this?
Found 2 solutions by Fombitz, MathTherapy:
Answer by Fombitz(32388)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! My daughter has a pre-algebra problem she nor I can figure out how to answer. The math problem is asking us to use the 5 step plan to solve it. Here is the written math problem to solve for:
What are the possible lengths and wideths of arectangle if its length is 8 centimeters longer than the width, and the area is less than or equal to 33 square centimeters?
a. Identify.
b. Strategize.
c. Set up.
d. Check.
We both came to the conclusion that since L x W = A that the Width must be 3 and the Length must be 11 because 11 x 3 = 33 since the problem states that the area must be less than or equal to 33 square cm. And since it states that the Length is 8 centimeters longer than the width we know that if 3 is the width then adding 8 to 3 = 11. Only problem is we do not understand how to set this up as an equation to solve through the 5 step plan. How do we do this?
This is NOT an EQUATION, but an INEQUALITY instead
Let width be W
Then length = W + 8
Area: W(W + 8), or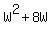 
We then get: 
Width or  OR W ≤ - 11 (ignore)
Thus, if width (W) = 3, then length = 3 + 8, or 11
If width (W) = 2, then length = 2 + 8, or 10
In other words, your width MUST BE EQUAL to or less than 3. Whatever value you assign to W, or width, you add 8 to that value to get the length.
Note that width, or 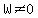 , or CANNOT be LESS than 0, so the range of values for the width is: 
|
|
|
