Question 999839: A soccer stadium holds 31,000 spectators. With a ticket price of $11, the average attendance has been 13,000. Market research has shown that for every $2 reduction in price, attendance will rise by 2,500. Assuming that attendance is linearly related to ticket price, what ticket price would maximize revenue?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! first you want to create the formula for attendance.
this will be a straight line equation.
when x = 11, attendance is 13000
when x = 9, attendance is 15500
these are two coordinate points on your graph.
(x1,y1) is the first point.
(x2,y2) is the second point.
you have:
(x1,y1) = (11,13000)
(x2,y2) = (9,15500)
the slope intercept form of the equation for a straight line is y = mx + b.
m is the slope
b is the y-intercept.
given two points, m = (y2-y1) / (x2-x1).
this becomes (15500 - 13000) / (9 - 11) = 2500 / -2 = -1250
your slope is -1250.
y = mx + b becomes y = -1250x + b
to find b, take any coordinate point on the line and replace y with the y-coordinate and replace x with the x-coordinate and solve for b.
we'll use (x1,y1) = (11,13000)
y = -1250x + b becomes 13000 = -1250*11 + b
solve for b to get b = 13000 + 1250*11 = 26750
y = -1250x + b becomes y = -1250x + 26750.
that is the equation for attendance.
the graph of that equation is shown below:
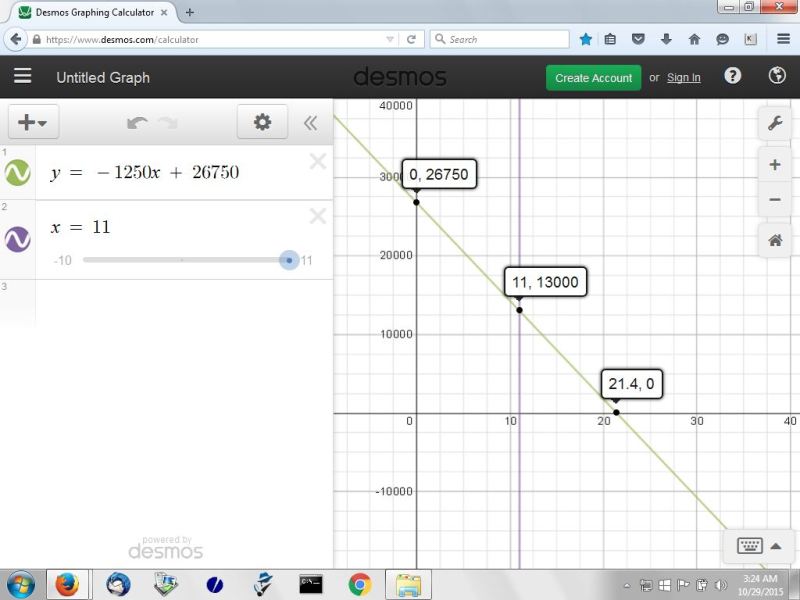
based on the formula, you can see on the graph that:
when x = 0, attendance is 26750.
when x = 21.4, attendance is 0.
when x = 11, attendance is 13000.
not shown on the graph, but calculated from the formula, you also get:
when x = 9, attendance is 15000, confirming that the equation is good.
revenue is equal to attendance times price.
let y = revenue
let x = price
let -1250x + 26750 = attendance
equation becomes:
y = (-1250x + 26750) * x
you can graph this equation as is, or you can simplify it to get:
y = -1250x^2 + 26750x
you will get the same graph either way.
you can find the maximum value of y from the graph, or you can derive it from the quadratic equation formula of x = -b/2a and y = f(-b/2a)
in the equation of y = -1250x^2 + 26750x:
a = -1250
b = 26750
x = -b/2a = -26750 / -2500 = 10.7
f(-b/2a) becomes f(10.7)
replace x in the equation with 10.7 and you get:
y = -1250*10.7^2 + 26750*10.7 = 143112.5 which is shown as 143113 on the graph.
that is the maximum revenue that can be attained based on the formula.
the graph of the revenue equation is shown below:
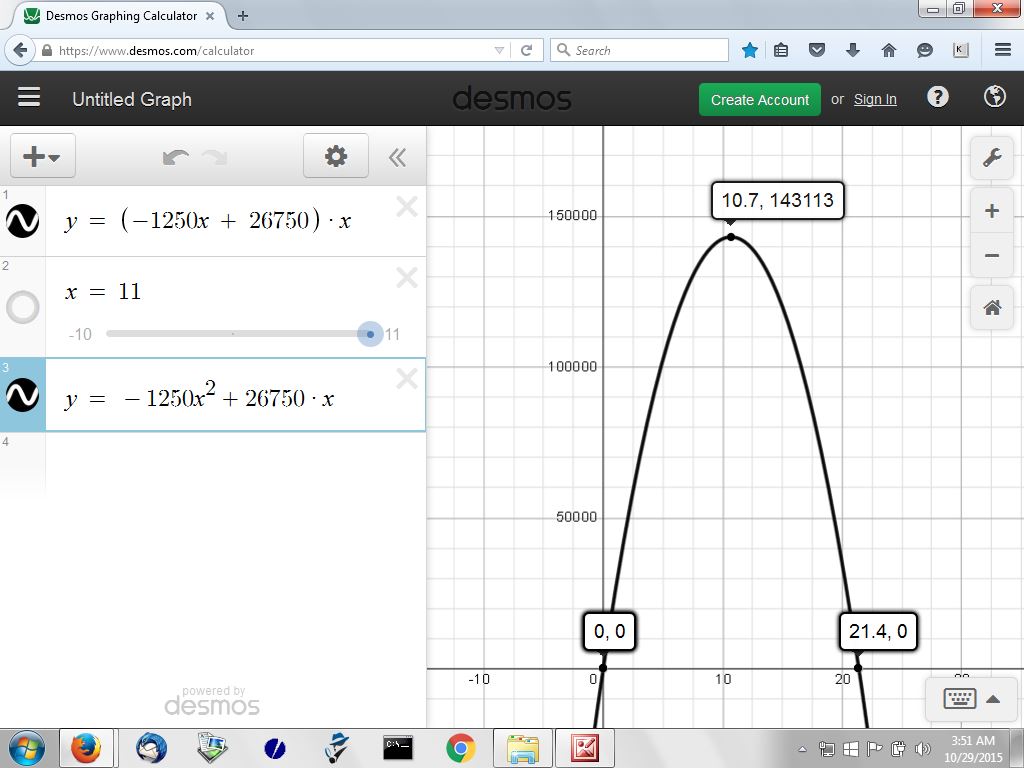
|
|
|