Question 999181: A forest ranger is in a forest 2 miles from a straight road. A car is located c miles down the road. The forest ranger can walk 2 miles per hour in the forest and travel 4 miles per hour along the road. In the picture below, the forest ranger walks in a straight line to a point x unit from the end of the road on the left, and then along the road.
http://imgur.com/kz9fJqj
The total travel time for the ranger to get to the car is the sum of the travel time in the forest and the travel time on the road. Write the total time T as a function of x, using the letter c for the distance from the end of the road on the left to the car.
T(x) = ?
Toward what point on the road should the ranger walk in order to minimize the travel time to the car if...
(a) c = 9 miles? (Numerical Answer ONLY)
x = ?
(b) c = 1/2 miles? Remember that the point must lie between the left end of the highway and the car. (Numerical Answer ONLY)
x = ?
Please explain how to solve this
Thank you
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! The path he takes through the forest is the hypotenuse of the right triangle at the left of the picture, having legs x and 2. This hypotenuse is 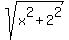 . .
The distance of the path along the road will be  . .
Basic uniform travel rates rule says, RT=D, or T=D/R. Implied variables' meanings.
T also will be for "time", which is mostly what the problem description is for. The ranger's travel time as a function according to the different rates will be
 ; ;
Later, you will use two different values for c, but for first dealing with the function, maintain as the variable.
To look for minimized travel time, find dT/dx and equate to 0; and then solve for x.
Just the beginning of that process:





The rest of this first part is to set the derivative equal to 0, and solve for x, looking for what x makes the minimum time.
|
|
|