Question 999074: Gery wants to fence a rectangular field whose area is 1200 sq.m. He has only 100 meters of fencing so he decided to fence only the three side of the rectangle letting the wall be the fourth side. How wide the rectangle should be?
Found 2 solutions by MathLover1, fractalier:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Gery wants to fence a 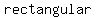  whose area is whose area is  . .
if the length is  and the width is and the width is  , than the area is: , than the area is:

 .............eq.1 .............eq.1
if he has only  of fencing and he decided to fence only the three side of the rectangle letting the wall be the fourth side, then we have of fencing and he decided to fence only the three side of the rectangle letting the wall be the fourth side, then we have
 ....solve for ....solve for 
 ......eq.2 ......eq.2
go to
 .............eq.1 substitute .............eq.1 substitute 
 .......solve for .......solve for 
 ...both sides divide by ...both sides divide by 








so, the width is:
 => => or or
 => =>
if  .............eq.1 and .............eq.1 and  , then the length is: , then the length is:



or, if  , we have , we have



so, there are two possible solutions:
 and and 
or
 and and
since he is going to fence only tree sides, one length and two width, and he has  of fence, we will see do both solution from above satisfies requirement: of fence, we will see do both solution from above satisfies requirement:
 ....if ....if  and and 


 => it satisfies requirement => it satisfies requirement
 ....if ....if  and and 


 => it satisfies requirement => it satisfies requirement
so, the rectangle should be 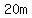 or or 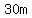 wide wide
Answer by fractalier(6550)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here you know length times width is 1200, or
LW = 1200
You also know that
L + 2W = 100
Solve this for L and substitute into the first equation to get
L = 100 - 2W and
(100 - 2W)W = 1200
100W - 2W^2 = 1200
Gather like terms and simplify...
2W^2 - 100W + 1200 = 0
W^2 - 50W + 600 = 0
We can factor this as
(W - 20)(W - 30) = 0
and so
W = 20 and L = 60
OR
W = 30 and L = 40
Two solutions!
|
|
|