Question 998253: 1) A truck has a shipment of 500 I-phones. If there are 9 defective I-phones on the truck, what is the probability of picking 12 I-phones at random and getting 3 defective I-phone?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given:
N=500 i-phones of which k=9 are defective
A random sample of n=12 is taken.
Need to know the probability that r=3 are defective in the sample.
Solution:
This problem seems to be a binomial distribution where
p=k/N=0.018
n=12, and
r=3
and C(n,r)=n!/(r!(n-r)!) (# of combinations of r objects out of n)
giving the probability of r=3 being defective out of sample size n=12:
P(3 out of 12)
=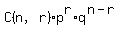
=
=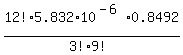
=0.00109
However, if we examine the conditions of applicability of the binomial theorem, we find that not all conditions are satisfied.
The experiment having 12 steps, the probability of picking a defective phone changes from one step to the other. The relatively large population gives the impression that it is relatively constant, but the small number of defectives does the reverse. Each defective picked decreases the probability by at least 10%.
The real answer to this problem is using the hypergeometric distribution, which is
Population size, N = 500
sample size, n = 12
total number of defectives (successes), k = 9
number of "successes" = 3
P(3 out of 12) = 
=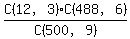
=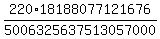
= 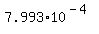
(about three quarters of the value obtained by binomial)
Answer:
Probability = 0.00109 (approximation using binomial distribution)
Probability = 0.00080 (using the Hypergeometric distribution)
|
|
|