Question 997637: Given the equation  , for what values of k will the equation have a repeated root, 2 real roots, and 3 values of k that will give the equation rational roots. I understand what it means to have those types of roots, I just don't understand how you would get to those specific answers. Like, I know how to find and imaginary root for this equation: , for what values of k will the equation have a repeated root, 2 real roots, and 3 values of k that will give the equation rational roots. I understand what it means to have those types of roots, I just don't understand how you would get to those specific answers. Like, I know how to find and imaginary root for this equation:  . Would that be right? . Would that be right?
Found 3 solutions by josgarithmetic, Boreal, MathLover1:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! 4x^2+8x+k=0
4x^2+8x=-k
Factor out 4.
4(x^2+2x)= -k but k can be any constant, so it doesn't have to be divided by 4.
If you complete the square, the roots will be the same, -1.
4(x^2+2x+1)= -(k)+4, adding 4 to both sides
4(x+1)^2= -k +4
The right side has to equal zero for completing the square to give two roots of -1
-k=-4
k=4
4x^2+8x+4=0
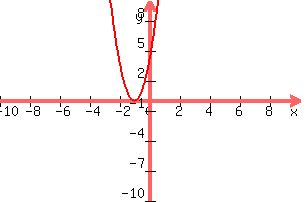
========
Two real roots can be many things, so long as the discriminant b^2-4ac is positive.
b^2>4ak, since k is acting as c
64>16k
k<4 will work

=========
Rational roots work if the discriminant gives a perfect square, for all parts of the quadratic formula will be a fraction with nothing but integers.
b^2-16k has to be a perfect square
64-16k
k=0 works and roots are 4 and 0
k=3 :(1/8){-8 +/- sqrt(16){=(1/8)(-4) and (1/8)(-12)
k= -36/16 (1/8) (-8 +/- sqrt (100) and (1/8)(-8+10), (1/8) (-8-10) or (10/8), (-18/8)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given the equation  , for what values of , for what values of  will the equation have a will the equation have a  root (one double root), root (one double root),  real roots, and real roots, and  values of k that will give the equation rational roots. values of k that will give the equation rational roots.
First of all, every polynomial has a discriminant, not just quadratics. The discriminant is the first place you look to classify the types of roots a polynomial has.
For example, a quadratic equation ax^2 + bx + c = 0, has a discriminant 
If 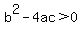 , there are , there are  real roots. real roots.
If  there are two imaginary roots . there are two imaginary roots .
If  , there is , there is 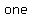 repeated root. repeated root.
so, in your case we have
 where where  , ,  , and , and 
If 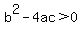 , there are , there are  real roots. real roots.
so,
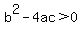
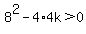
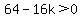
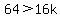
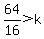
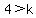 or or
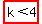
take first number less then  : : and check the roots and check the roots
 ...when you check it, you will find out that roots are: ...when you check it, you will find out that roots are:  and and 

If  there are two imaginary roots . there are two imaginary roots .


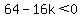
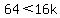
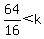
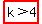
take  and check and check

If  , there is , there is 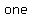 repeated root. repeated root.






take  and check and check
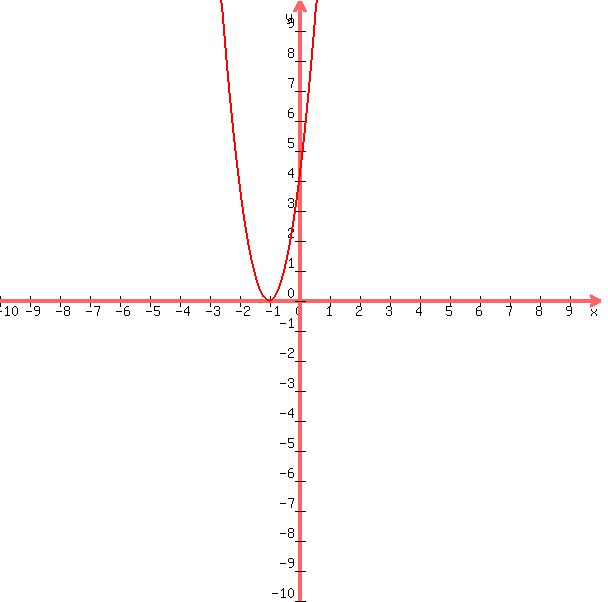
|
|
|