Question 997445: A field bordering a straight stream is to be enclosed and divided in 2. The side of bordering the stream does not need to be fenced.
If 2400 yards of fencing is to be used, give an equation for the perimeter of the field (middle part must be included).
Give an equation for the area of the field.
Rewrite the equation for area so that it contains only one independent variable.
What are the dimensions of the largest rectangular field that can be enclosed? Find algebraically using the vertex.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let w = the width
let l = the length
perimeter = l + 3w
the perimeter is equivalent to the amount of fencing required.
because the property is divided into two pieces, there are 3 widths rather than 2, the third width being the partition in the middle.
since perimeter = 2400, the formula for perimeter becomes:
2400 = l + 3w
the area formula is:
area = l * w
this is the area of the enclosure which includes both halves.
since 2400 = l + 3w, we can solve for l to get l = 2400 - 3w
formula for area = l * w becomes area = (2400 - 3w) * w
remove parentheses to get area = 2400w - 3w^2
this is a quadratic equation.
rearrange the terms to get area = -3w^2 + 2400w
set this equation to 0 to get -3w^2 + 2400w = 0
this is in standard quadratic equation form of aw^2 + bw + c = 0
a is the coefficient of the w^2 term, b is the coefficient of the w term, c is the constant term.
we get:
a = -3
b = 2400
c = 0
the formula for the value of w that provides maximum point on this equation is:
w = -b/2a
the maximum point on this equation is the maximum area of the enclosure.
this results in w = -2400 / -6 which is equal to 400.
the area is maximized when w = 400.
when w = 400, the area is equal to 2400w - 3w^2 which becomes 2400*400 - 3*400^2 which results in an area of 480,000 square yards.
when w = 400, l = 1200 because 2400 = 1200 + 3 * 400.
your solutions are:
perimeter = 2400 = l + 3w
area = l*w
area = (2400 - 3w) * w which is equal to 2400w - 3w^2.
largest area is when w = 400 and l = 1200.
w is the width of the enclosure.
l is the length of the enclosure.
l is the letter L, not to be confused with 1 which is the number one.
they are unfortunately very close in appearance with the number 1 having a slanted tip on the top while the letter l has a horizontal tip on the top.
otherwise they are identical.
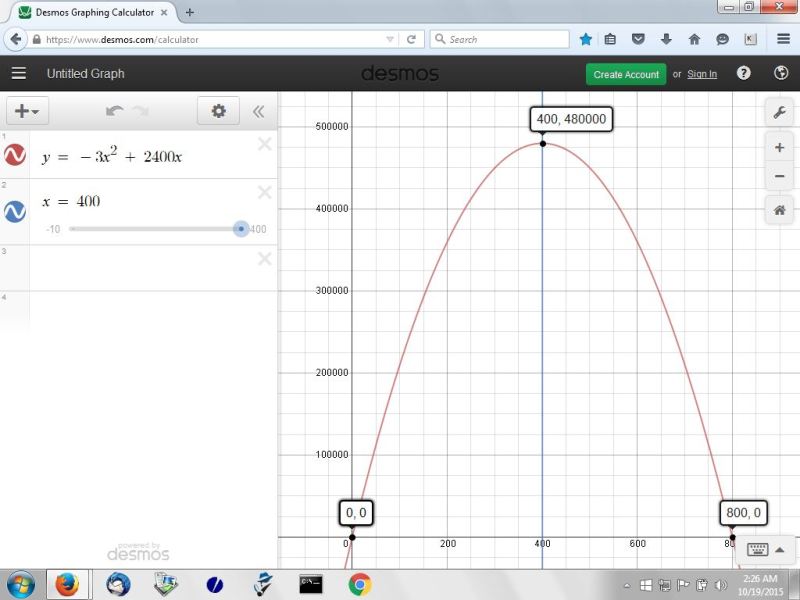
here's a graph of the equation for the area so you can see what the qaution looks like when graphed.
to graph the equation, the area is represented by y and the width is represented by x.
it's easy to see from the graph that the maximum area is when x = 400.
|
|
|