Question 99741: Factor completely using integer coefficients:
e) x^4+8x^3-2x^2-16x
f) 2x^6-20x^4-16x^3+160x
j) x^4-x^3-x+1
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Factor completely using integer coefficients:
e) 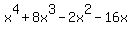 First, factor an x. First, factor an x.
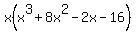 Now factor the parentheses. I know that my factors here will be two binomials of the form: Now factor the parentheses. I know that my factors here will be two binomials of the form:
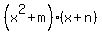 where where  and and  and and  , so m = -2 and n = 8. So the parentheses, when factored, look like: , so m = -2 and n = 8. So the parentheses, when factored, look like:
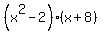 , then the final answer is: , then the final answer is:

f) 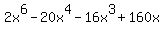 First, factor 2x. First, factor 2x.
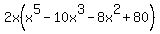 Now factor the parentheses. I know my factors here will be two binomials of the form: Now factor the parentheses. I know my factors here will be two binomials of the form: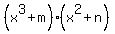 where: where:   and and  so so  and and  , so the parentheses, when factored, look like: , so the parentheses, when factored, look like:
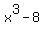 , so far we have: , so far we have:
 but notice that but notice that 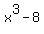 is the difference of two cubes and this can be factored. is the difference of two cubes and this can be factored.
 The difference of two cubes is factored thus: The difference of two cubes is factored thus:
 so, in this case: so, in this case:
 putting it all together, we have: putting it all together, we have:

j) 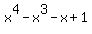 Factor as: Factor as:
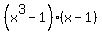 But again, we have the difference of two cubes: But again, we have the difference of two cubes: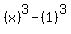 , so... , so...
 or: or:

|
|
|