SOLUTION: If you know that -2 is a zero of f(x)=x^3+7x^2+4x-12, explain how to solve the equation x^3+7x^2+4x+12=0. Also give an explanation to why x-2 is or is not a factor

Algebra ->  Finance -> SOLUTION: If you know that -2 is a zero of f(x)=x^3+7x^2+4x-12, explain how to solve the equation x^3+7x^2+4x+12=0. Also give an explanation to why x-2 is or is not a factor      Log On


   

Question 997336: If you know that -2 is a zero of f(x)=x^3+7x^2+4x-12, explain how to solve the equation x^3+7x^2+4x+12=0.
Also give an explanation to why x-2 is or is not a factor
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%29=x%5E3%2B7x%5E2%2B4x-12
if x%5B1%5D=-2 is a zero, means f%28x%29=x%5E3%2B7x%5E2%2B4x-12 is divisible by x-x%5B1%5D=x-%28-2%29=x%2B2->an explanation to why x-2 is not a factor
use long division:
---------(x%5E2%2B5x-6
x%2B2|x%5E3%2B7x%5E2%2B4x-12
----------x%5E3%2B2x%5E2.......subtract
------------0%2B5x%5E2......add 4x
------------- 5x%5E2%2B4x......
------------- 5x%5E2%2B10x.......subtract
-------------- 0-6x.......add -12
--------------- -6x-12.......
--------------- -6x-12.......subtract
----------------- 0.......reminder
so, now we know two factors of given polynomial, and they are x%2B2 and x%5E2%2B5x-6
so, you have
f%28x%29=%28x%2B2%29%28x%5E2%2B5x-6%29 ...now we can factor x%5E2%2B5x-6 too
f%28x%29=%28x%2B2%29%28x%5E2%2B6x-x-6%29
f%28x%29=%28x%2B2%29%28%28x%5E2%2B6x%29-%28x%2B6%29%29
f%28x%29=%28x%2B2%29%28x%28x%2B6%29-%28x%2B6%29%29
f%28x%29=%28x%2B2%29%28x-1%29%28x%2B6%29

so, zeros are:
if 0=%28x%2B2%29=>x=-2
if 0=%28x-1%29=>x=1
if 0=%28x%2B6%29=>x=-6

+graph%28+600%2C+600%2C+-10%2C+10%2C+-15%2C+15%2C+x%5E3%2B7x%5E2%2B4x-12%29+


Answer by MathTherapy(10556) About Me  (Show Source):
You can put this solution on YOUR website!

If you know that -2 is a zero of f(x)=x^3+7x^2+4x-12, explain how to solve the equation x^3+7x^2+4x+12=0.
Also give an explanation to why x-2 is or is not a factor
f%28x%29+=+x%5E3+%2B+7x%5E2+%2B+4x+-+12

Itw's given that - 2 is a zero

Using synthetic division, we get:

  - 2| 1    7    4  - 12 
     |_____-2 - 10    12  
       1    5  - 6     0

Since - 2 is a zero, then x = - 2, and x + 2 = 0, so x + 2 is a factor

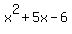
We now get: f%28x%29+=+%28x+%2B+2%29%28x%5E2+%2B+5x+-+6%29

f%28x%29+=+%28x+%2B+2%29%28x+%2B+6%29%28x+-+1%29 ------- Factoring x%5E2+%2B+5x+-+6

0+=+%28x+%2B+2%29%28x+%2B+6%29%28x+-+1%29

Therefore, highlight_green%28system%28x+=+-+2_OR%2Cx+=+-+6_OR%2Cx+=+1%29%29


If x - 2 is a factor, then x - 2 = 0, and so, x = 2 (one of the zeroes)

If x - 2 is a factor, then 2 (one of the zeroes) should NOT produce a remainder when the Remainder theorem: is used.

Remainder theorem: f%28x%29+=+x%5E3+%2B+7x%5E2+%2B+4x+-+12

Therefore, we get: f%282%29+=+2%5E3+%2B+7%282%29%5E2+%2B+4%282%29+-+12
 
f%282%29+=+8+%2B+28+%2B+8+-+12

f%282%29+=+32

With f(2) = 32, a remainder exists, and so, x - 2 is NOT a factor