Question 997244: I don't know if this is the right topic?
Question: A stationary car, a, is passed by car b moving with a uniform velocity of 25m/s. Five seconds later, car a starts moving with a constant acceleration of 2m/s^2 in the same direction.
Construct a pair of simultaneous equations and plot on a graph using a spreadsheet to find how long it will take car a to draw level.
I have tried to do this question but I don't know how to work out a pair of simultaneous equations I have got a quadratic 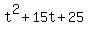 . Not sure how to put that into a spreadsheet to make a graph. I used the equation  and substituted the values from car a and car b in and came up with 2 formulas  for car a and  I then made them equal to each other and subtracted 5 seconds of car a making it  due to it starting 5 seconds later. This is how I came to the equation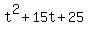
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! You almost solved it, but not the way the problem specified.
With  = time in seconds from the moment car B passes car A
The distance from the point where car B passed car A is
 for car B (for  , because we do not know what car B was doing before), and
 for car A for  .
(Of course, for   because car A was not moving then).
So when A is level with B again,  , and
 ---> ---> .
The solutions to that equation, using the infamous quadratic formula are
 .
Since 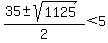 , it is not a solution to our problem.
The solution to our problem is
(You had a little problem with  and  signs, but I make those mistakes sometimes, so that proves that we are both human).
WHAT THE TEACHER WANTS (I think):
Here is how I would answer if it was my homework.
= time in seconds from the moment car B passes car A.
for is the distance traveled by car A since B passes it.
(for is the distance traveled by car B after it passes car A.
So, for , the system of simultaneous equations that describes the situation in the problem is
 .
I used Microsoft Excel to tabulate and plot as shown below:
 
|
|
|
