Question 996115: An object thrown from a planet an altitude of 1449 ft. The initial velocity is 16ft/s. How many seconds later will the object strike the ground?
Hooblah1991@gmail.com
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If that planet is Earth, or you meant "thrown from a plane", and the object is thrown downwards, I have an answer.
The acceleration of gravity for objects as close to Earth's surface as non-astronauts ever get is   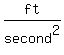 . .
With an initial downward velocity of  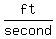 , ,
the downwards velocity (in ft/s) for a heavy enough object
would be  , ,
as a function of time,  (in seconds) since the object was thrown. (in seconds) since the object was thrown.
NOTE:
In real life, some objects (like a helium filled balloon) will not fall like that, because buoyancy makes the downward "weight" force less than mass times  . .
Also, even for heavy enough objects, air drag will eventually stop the velocity increase,
and a constant velocity (terminal velocity) will be asymptotically approached.
IF WE CAN DISREGARD THE EFFECTS OF BUOYANCY AND AIR DRAG:
The average velocity for the first  seconds is seconds is
 . .
The distance (in ft) the object travels over  seconds is seconds is
 . .
When the object has traveled 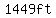 downwards, downwards,
it strikes the ground, and
 <---> <---> . .
Solving that quadratic equation, we find

IF WE HAVE TO CONSIDER AIR DRAG AND/OR BUOYANCY:
It will take longer for that object to strike the ground,
but it is a more complicated calculation,
and it depends on the "drag coefficient" of the object,
and that depends of the shape
With high terminal velocities of about 90 m/s (about 300 ft/s) reported (for a bullet),
it is likely that drag would be a factor, because without it,
after 9 seconds the velocity (in ft/s) would be
 ft/s. ft/s.
|
|
|