|
Question 995853: Lisa can fill a order in 9 hours. Tom can fill an order in 10 hours. How long will it take working together for them to fill the order?
Answer by ikleyn(52802)   (Show Source):
You can put this solution on YOUR website! .
Lisa can fill a order in 9 hours. Tom can fill an order in 10 hours. How long will it take working together for them to fill the order?
-------------------------------------------------------------------------
Since Lisa can complete the order in 9 days, she is completing  of the job per hour.
Since Tom can complete the job in 10 days, he is completing  of the job per hour.
So, working together, Lisa and Tom can complete  of the job per hour.
Now you need to calculate this sum of two fractions, . It requires standard operations:
- to convert fractions to a common denominator, which is equal to 90 in this case;
- then add numerators;
- then reduce the resulting fraction if possible:
=  =  =  .
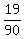Thus, working together, Lisa and Tom can complete 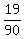of the order per hour.
Hence, it will take 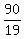 =   hours for Lisa and Tom to complete this job working together.
Answer. Working together, Lisa and Tom can complete the job in hours.
See the lesson Using fractions to solve word problems on joint work in this site for more rate-of-work problems.
|
|
|
| |
